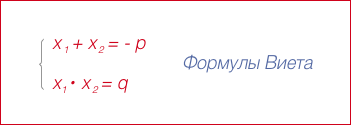Формула Вієта: Теорема як основа розв’язання квадратних рівнянь
Формула Вієта є однією з найвідоміших і найкорисніших теорем в алгебрі, що зв’язує коефіцієнти квадратних рівнянь з їх коренями. Дана формула дозволяє швидко знаходити суму і добуток коренів без фактичного розв’язання рівняння, що значно полегшує математичний аналіз і розрахунки.
Історичний контекст та розуміння формули Вієта
Формула, названа на честь французького математика Франсуа Вієта, є основним інструментом в алгебраїчних обчисленнях. Оригінально, Вієт працював над розвитком символічної нотації, яка зробила математику більш зрозумілою і доступною. Його робота створила основу для сучасної алгебри та аналітики.
Основні постулати формули Вієта
Формула Вієта представлена у формі залежності між коефіцієнтами квадратного рівняння і його коренями. Розглянемо квадратне рівняння загального вигляду:
ax² + bx + c = 0
Де a, b, і c — це коефіцієнти, а x₁ і x₂ — корені рівняння. Формула Вієта стверджує, що:
- Сума коренів: x₁ + x₂ = -b/a
- Добуток коренів: x₁x₂ = c/a
Ці дві прості формули можуть бути застосовані для перевірки правильності знайдених коренів, а також для визначення коефіцієнтів при заданих умовах.
Застосування формули Вієта
Сила формули Вієта полягає в її здатності знаходити відсутні параметри в алгебраїчних рівняннях та задачах. Наприклад, якщо відомі корені рівняння, але не відомі його коефіцієнти, можна використовувати формулу Вієта для їх обчислення.
Приклад застосування:
- При заданих коренях x₁ = 2 та x₂ = 3, визначити коефіцієнти
- Використовуємо суму коренів: 2 + 3 = -b/a = 5 ⟹ b = -5a
- Використовуємо добуток коренів: 2 * 3 = c/a = 6 ⟹ c = 6a
Таким чином, коефіцієнти рівняння можуть бути виражені через a, де a є довільним числом (найчастіше обирається одиницею для простоти).
Таблиця сум і добутків
| Коефіцієнт | Значення |
|---|---|
| a | 1 (звичайний випадок) |
| b | -(x₁ + x₂) |
| c | x₁x₂ |
Висновок
Формула Вієта є важливою складовою частиною алгебраїчної теорії, забезпечуючи швидкий і надійний спосіб роботи з квадратними рівняннями. Ефективність цього математичного інструменту вражає своєю простотою та універсальністю, що робить його незамінним для тих, хто займається наукою чи технікою.