Теорема Дискримінант: Основа Аналізу Квадратних Рівнянь
Теорема дискримінант відіграє ключову роль в аналізі квадратних рівнянь, надаючи можливість швидко та точно визначити кількість і тип коренів без їх безпосереднього обчислення. Цей фундаментальний метод є невід’ємною частиною алгебри і широко використовується для спрощення вирішення задач та систематизації математичних знань.
Що таке Теорема Дискримінант?
Дискримінантом квадратного рівняння називається вираз:
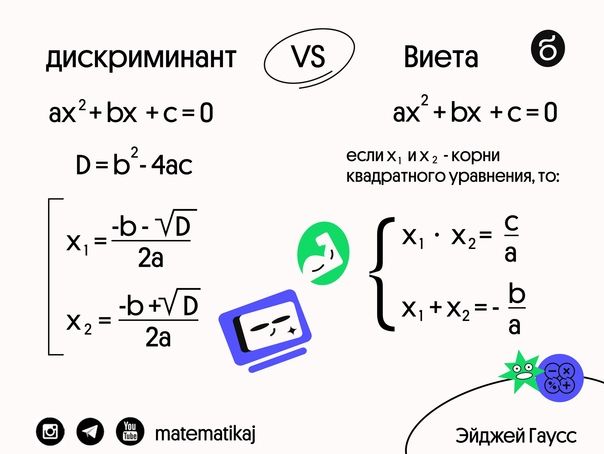
D = b² – 4ac, де
- a, b, c — коефіцієнти квадратного рівняння ax² + bx + c = 0.
Теорема дискримінант дозволяє виявити наступні властивості коренів рівняння залежно від значення D:
- Якщо D > 0, рівняння має два різних дійсних кореня.
- Якщо D = 0, рівняння має один дійсних корінь, який є подвійним.
- Якщо D < 0, рівняння не має дійсних коренів, а лише комплекснозначні.
Значення Теореми Дискримінант в Математиці
Теорема дискримінант надає ряд математичних і практичних переваг:
- Ефективність розв’язання: Опрацювання коренів рівняння за допомогою дискримінанту є більш швидким та зрозумілим процесом, ніж традиційні методи розв’язання.
- Розуміння структури: Вона допомагає зрозуміти, як коефіцієнти рівняння впливають на його розв’язок та властивості.
- Систематизація знань: Теорема є важливим інструментом для вивчення більш складних алгебраїчних структур та систем.
Взаємозв’язок з Теоремою Вієта
Теорема дискримінант часто використовується поряд з теоремою Вієта, яка визначає взаємозв’язок між коренями квадратного рівняння та його коефіцієнтами:
- Сума коренів: ( x_1 + x_2 = -frac{b}{a} )
- Добуток коренів: ( x_1 cdot x_2 = frac{c}{a} )
Поряд із дискримінантом, теорема Вієта формує основу для глибшого розуміння та аналізу квадратних рівнянь.
Приклад Використання Теореми Дискримінант
Розглянемо квадратне рівняння: ( 2x² – 4x + 2 = 0 ).
- Обчислюємо дискримінант: ( D = (-4)² – 4 cdot 2 cdot 2 = 16 – 16 = 0 ).
- Оскільки D = 0, рівняння має один корінь (подвійний):
- ( x = -frac{b}{2a} = -frac{-4}{2 cdot 2} = 1 ).
Заключення
Теорема дискримінант є невід’ємним компонентом для розв’язання та аналізу квадратних рівнянь. Вона не лише спрощує обчислення, але і надає глибше розуміння математичних зв’язків та процесів. У поєднанні з іншими теоретичними засобами, наприклад, теоремою Вієта, цей метод стає надзвичайно потужним інструментом для аналітичних досліджень у межах проблем алгебри та аналізу.