Формула довжина кола: Вступ до геометрії
В основі численних геометричних розрахунків лежить формула довжина кола. Це проста, але важлива формула, яка дозволяє нам визначити довжину будь-якого кола, знаючи лише радіус або діаметр цього кола. Її застосування поширюється від елементарних вправ у школі до складних наукових обчислень у різних галузях.
Що таке довжина кола?
Довжина кола – це лінійна відстань навколо кола, подібна до того, як периметр є відстанню навколо багатокутника. Визначення довжини кола є одним із основних завдань у геометрії та практично застосовується в різних сферах від архітектури до астрономії.
Формула для обчислення довжини кола
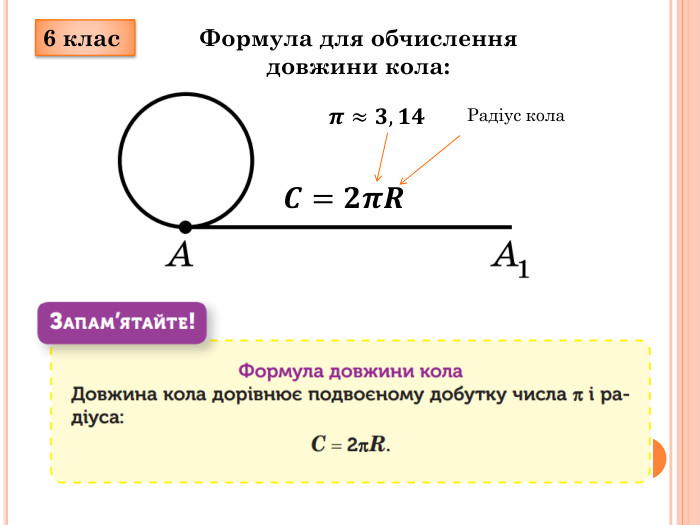
Формула довжина кола пов’язує довжину з її радіусом (r) або діаметром (d). Основна формула виглядає так:
- Якщо відомий радіус кола (r): L = 2πr
- Якщо відомий діаметр кола (d): L = πd
Де π (пі) – це математична константа, яка приблизно дорівнює 3.14159. Вона є ірраціональним числом, тобто його десяткове представлення нескінченне та не повторюється.
Важливі аспекти при використанні формули
- Радіус та діаметр: Пам’ятайте, що діаметр є вдвічі більшим за радіус, тобто d = 2r. Це спрощує переходи між формулами залежно від доступних у вас даних.
- Точність розрахунків: Використання значення π впливає на точність отриманого результату. У більшості практичних завдань достатньо використовувати 3.14, але для високоточного обчислення може знадобитися більше знаків після коми.
- Одиниці вимірювання: Переконайтеся, що використовуєте однакові одиниці вимірювання для всіх елементів формули, щоб отримати коректний результат.
Практичні приклади використання формули
Формула довжина кола використовується в широкому спектрі завдань:
| Сфера | Застосування |
|---|---|
| Будівництво | Розрахунок кількості матеріалу для круглих конструкцій |
| Машинобудування | Планування деталей машин круглої форми |
| Астрономія | Обчислення орбітальних параметрів планет |
Висновок
Розуміння та вірне використання формули довжина кола є ключовими як в освіті, так і в професійній діяльності. Вона не тільки полегшує виконання багатьох математичних задач, але й забезпечує міцну основу для більш складних геометричних та фізичних розрахунків. Незважаючи на її простоту, ця формула продовжує грати центральну роль у багатьох сучасних науках та техніках.