Формули Скороченого Множення: Значення та Практичне Застосування
Формула скороченого множення є важливою складовою частиною шкільного курсу математики, зокрема, алгебри. Вживання цих формул дозволяє значно полегшити обчислення та розв’язання широкого спектра задач. Розуміння того, як і коли їх застосовувати, допомагає учням уникнути складних обчислень, що особливо корисно при підготовці до іспитів або у вирішенні практичних завдань.
Що таке формули скороченого множення?
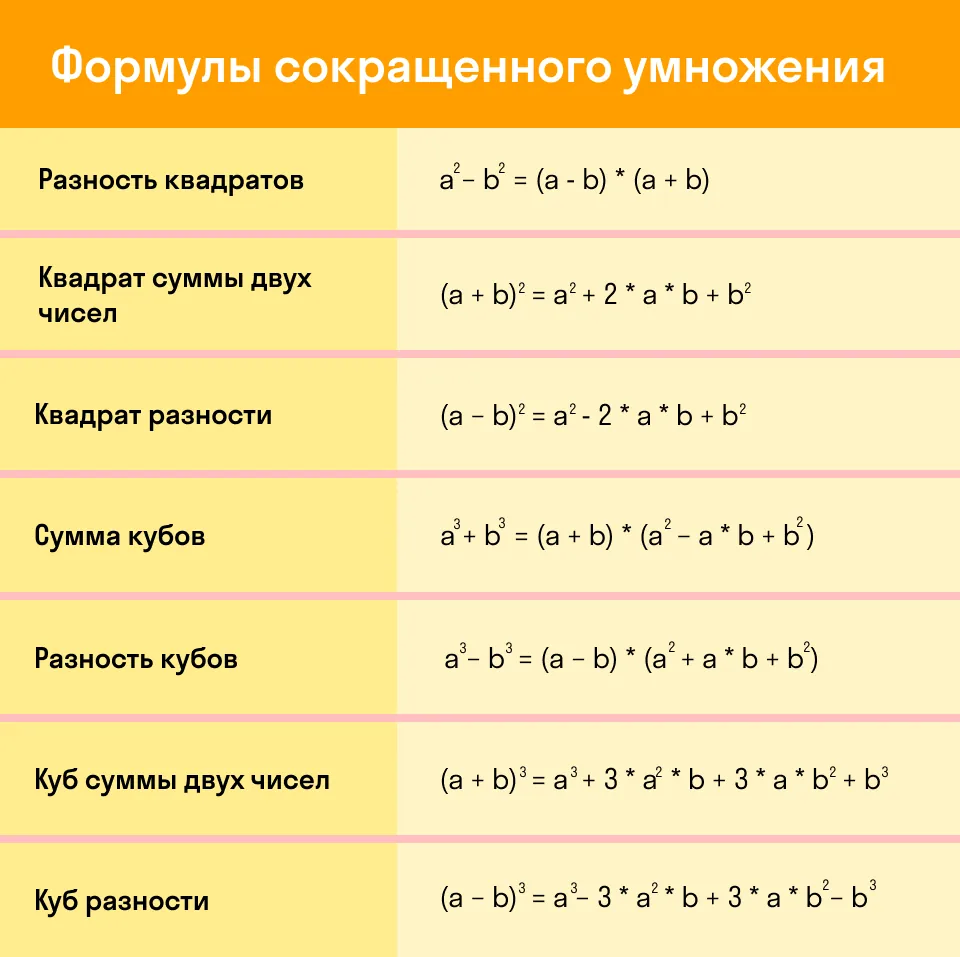
Формули скороченого множення — це певний набір математичних виразів, який дозволяє обчислювати квадрати, куби, різниці та суми виразів без розширеного множення. Ці формули розрізняють за типами, залежно від структури алгебраїчного виразу. Вони охоплюють такі популярні формули:
- Квадрат суми: (a + b)2 = a2 + 2ab + b2
- Квадрат різниці: (a – b)2 = a2 – 2ab + b2
- Різниця квадратів: a2 – b2 = (a – b)(a + b)
- Куб суми: (a + b)3 = a3 + 3a2b + 3ab2 + b3
- Куб різниці: (a – b)3 = a3 – 3a2b + 3ab2 – b3
Застосування у шкільних завданнях
Формули скороченого множення часто використовуються для спрощення виразів у задачах на алгебру. Розглянемо декілька прикладів їх застосування на практиці:
- Знайти значення виразу (x + 5)2:
Розв’язання: Використовуючи формулу квадрату суми, маємо:
(x + 5)2 = x2 + 2 * 5 * x + 25 = x2 + 10x + 25 - Спростити вираз (y – 3)(y + 3):
Розв’язання: Застосовуємо формулу різниці квадратів:
(y – 3)(y + 3) = y2 – 32 = y2 – 9
Практичні переваги
Систематичне застосування формул скороченого множення у обчисленнях тренує не лише навички спрощення алгебраїчних виразів, а й розвиває математичне мислення. Це особливо важливо, оскільки воно дозволяє:
- Економити час на виконання обчислень.
- Спрощувати складні задачі до більш зрозумілих форм.
- Розвивати креативний підхід до розв’язання задач.
| Формула | Опис |
|---|---|
| (a + b)2 | Квадрат суми двох чисел |
| (a – b)2 | Квадрат різниці двох чисел |
| a2 – b2 | Різниця квадратів |
| (a + b)3 | Куб суми двох чисел |
| (a – b)3 | Куб різниці двох чисел |
Вміння використовувати формули скороченого множення є необхідною навичкою для будь-якої людини, що прагне опанувати алгебру на високому рівні. Ці формули дозволяють не лише виконувати обчислення швидше, але й розширюють можливості для вирішення складних математичних задач.