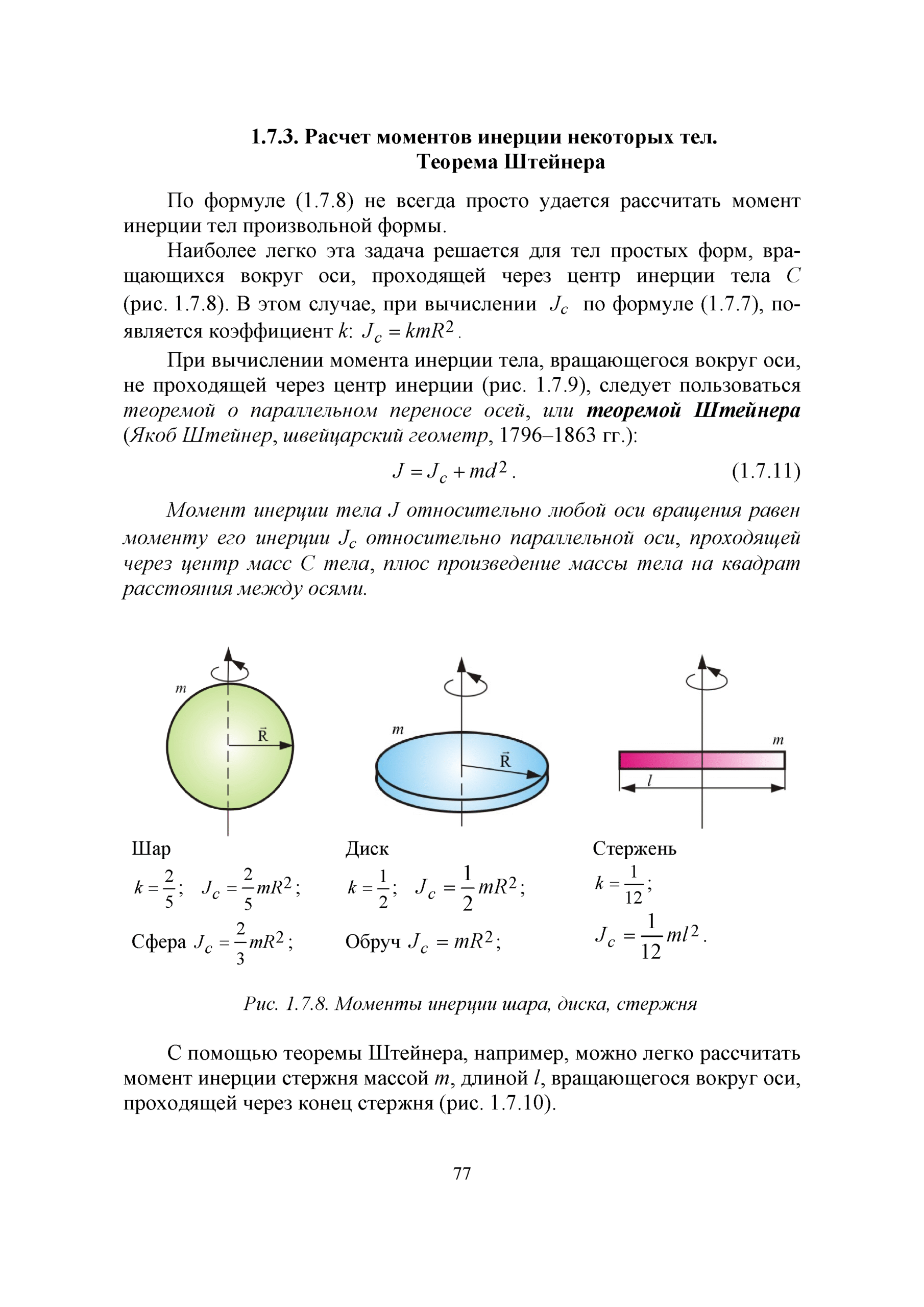
Теорема Штейнера: Основи, Застосування та Приклади
Теорема Штейнера, відома також як теорема про момент інерції, є важливим поняттям у фізиці, яке дозволяє визначити момент інерції тіла відносно будь-якої осі, якщо відомий момент інерції відносно паралельної осі, що проходить через центр маси тієї системи. Ця стаття покликана розповісти про особливості теореми Штейнера, її застосування та приклади.
Основи Теореми Штейнера
Теорема Штейнера формулюється таким чином: щоб визначити момент інерції тіла відносно певної осі, достатньо додати момент інерції цього тіла відносно осі, яка проходить через центр маси, та добуток маси тіла на квадрат відстані між цими осями.
I = Icm + md2- I — момент інерції відносно заданої осі.
- Icm — момент інерції відносно осі, яка проходить через центр маси.
- m — маса тіла.
- d — відстань між осями.
Застосування Теореми Штейнера
Теорема Штейнера широко застосовується у локалізації та аналізі різних механічних систем. Вона дозволяє ефективніше розраховувати моменти інерції, що є ключовим при вирішенні задач динаміки та статики.
Приклади застосування:
- Розрахунок моментів інерції частин механізмів при складних рухах.
- Аналіз структур будівель для визначення стійкості та міцності.
- Вивчення обертальних рухів планет та штучних супутників.
Приклади Розрахунків
Розглянемо приклад застосування теореми Штейнера для тонкого стержня, що обертається навколо осі, яка не збігається з його центром маси.
| Параметр | Значення |
|---|---|
| Довжина стержня (L) | 1 м |
| Маса стержня (m) | 2 кг |
| Відстань до осі обертання (d) | 0.5 м |
Розрахуємо момент інерції відносно осі, що проходить через край стержня:
Icm = (1/12) m L2 = (1/12) * 2 кг * (1 м)2 = 0.1667 кг м2Застосовуємо теорему Штейнера:
I = Icm + md2 = 0.1667 кг м2 + 2 кг * (0.5 м)2 = 0.6667 кг м2Висновок
Теорема Штейнера є незамінним інструментом в арсеналі інженера та фізика при розв’язанні задач, пов’язаних з моментами інерції. Завдяки ній, можна легко й швидко переходити від центрів маси до будь-яких обраних осей, отримуючи повну картину динамічного стану системи. Теорема Штейнера допомагає оптимізувати обчислення та покращити розуміння руху складних механічних структур. Вона представляє фундаментальний шматок у мозаїці, яку ми називаємо механікою.