Розуміння формули довжини вектора: Введення
У математиці та фізиці поняття вектора є надзвичайно важливим, особливо коли мова йде про опис руху, напряму або сили в просторі. Одним із ключових аспектів вивчення векторів є їх довжина, яка визначається за допомогою формули довжини вектора. Ця формула є засобом, що дозволяє точно вимірювати масштаби векторів у різноманітних технічних і наукових застосуваннях.
Що таке вектор?
Вектор — це математичний об’єкт, що має величину та напрям. На відміну від скалярів, які характеризуються лише величиною, вектори представляють величини, що мають як розмір, так і орієнтацію в просторі.
- Напрям: визначає, куди вектор “спрямований”.
- Величина (або довжина): описує, наскільки вектор “великий”.
Як визначається довжина вектора?
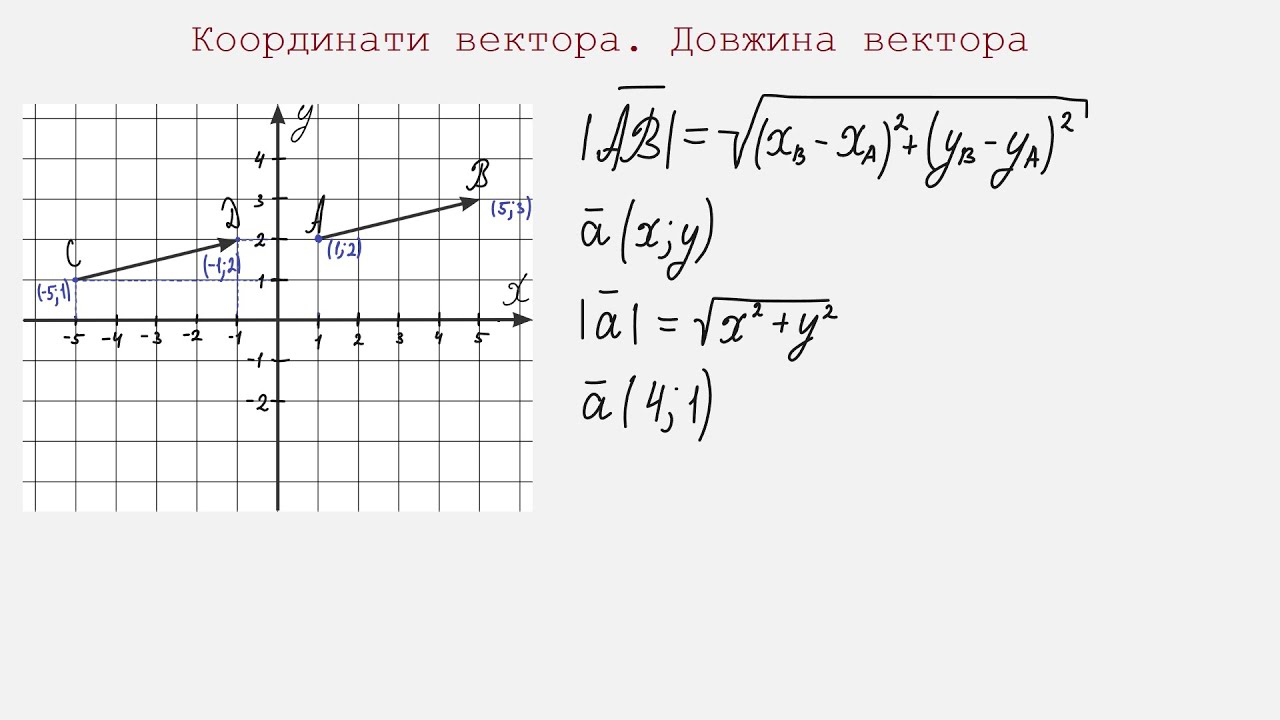
Довжина вектора, або його модуль, визначається за допомогою математичних розрахунків, що базуються на складових вектора. У просторі з трьома вимірами найчастіше використовують такий підхід:
- Ідентифікуйте складові вектора. Наприклад, вектор V в тривимірному просторі може бути представлений як V = (x, y, z).
- Застосуйте формулу довжини вектора:
| Формула | √(x² + y² + z²) |
|---|
Ця формула використовується для визначення довжини вектора в тривимірному просторі. Вона базується на теоремі Піфагора та є розширенням цієї теореми на багатовимірні простори.
Приклад застосування формули довжини вектора
Розглянемо приклад використання формули довжини вектора. Припустимо, у нас є вектор A з координатами A = (3, 4, 5). Щоб визначити довжину цього вектора, виконуємо наступні кроки:
- Застосовуємо формулу: √(3² + 4² + 5²)
- Обчислюємо квадрати складових: 9 + 16 + 25 = 50
- Знаходимо квадратний корінь: √50 ≈ 7.07
В результаті, довжина вектора A становить приблизно 7.07 одиниць.
Практичні аспекти використання формули
Знання про формулу довжини вектора є важливим у багатьох прикладних дисциплінах. Наведемо кілька прикладів:
- Фізика: розрахунок швидкості або сили об’єкта.
- Інформатика: обробка векторних даних у графічних програмах чи іграх.
- Інженерія: моделювання векторних сил у конструкторських розрахунках.
Таким чином, вивчення та розуміння векторів, зокрема їх довжини, є невід’ємною частиною розвитку аналітичних та технічних навичок. Це знання формує базис для багатьох функціональних і технологічних досягнень сучасного світу.