Формула прямокутного трикутника та її застосування
Формула прямокутного трикутника є фундаментальним елементом геометрії, яка знаходить своє застосування як в академічному, так і в практичному житті. Зокрема, вивчення площі та периметра прямокутного трикутника, його сторін і кутів є надзвичайно важливим для розуміння більш складних геометричних концепцій.
Основні елементи прямокутного трикутника
Прямокутний трикутник має кілька важливих складових, розуміння яких є критичним для опанування цього розділу геометрії. До таких елементів відносяться:
- Катети: Дві сторони, які формують прямий кут.
- Гіпотенуза: Сторона, протилежна прямому куту, яка є найдовшою стороною в трикутнику.
- Прямий кут: Кут у 90 градусів, що є характерною ознакою прямокутного трикутника.
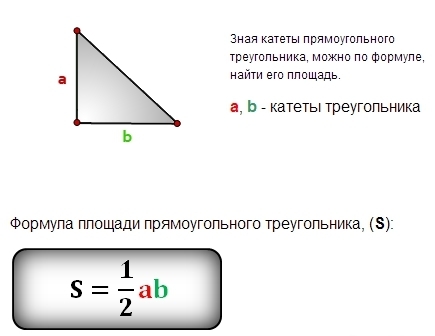
Формула площі прямокутного трикутника
Площа прямокутного трикутника обчислюється за допомогою формули, яка передбачає добуток довжин обох катетів, поділений на два:
| Формула площі | S = (a * b) / 2 |
|---|
Де S – площа прямокутного трикутника, a та b – довжини катетів. Ця формула є корисною не лише в академічних умовах, але й у повсякденності, наприклад, при обчисленні площ, які є частинами більших структур.
Периметр прямокутного трикутника
Периметр прямокутного трикутника обчислюється шляхом підсумовування довжин його трьох сторін. Формула виглядає наступним чином:
| Формула периметра | P = a + b + c |
|---|
Де P – периметр трикутника, a, b – катети, а c – гіпотенуза.
Відношення сторін прямокутного трикутника: теорема Піфагора
Важливим математичним відношенням у прямокутному трикутнику є теорема Піфагора, що встановлює зв’язок між довжинами сторін. Теорема стверджує:
| Теорема Піфагора | c² = a² + b² |
|---|
- Де c – довжина гіпотенузи
- a та b – катети
Цей принцип використовується для обчислення невідомих сторін, тестування правильності встановлених даних та багато іншого.
Практичні застосування формули прямокутного трикутника
Розуміння формули прямокутного трикутника надає значні переваги у багатьох галузях, від будівництва до інженерії. Ефективне використання цих знань дозволяє розв’язувати задачі з площами, вимірювати кути і довжини в різних конструкціях, забезпечуючи точність і надійність у будь-яких обчисленнях.
Формула прямокутного трикутника є важливим інструментом для сучасних інженерів, архітекторів, та інших спеціалістів, які працюють із геометричними формами в практичних умовах. Завдяки її універсальності, ця формула залишається одним із найцінніших засобів у світі математики та науки загалом.