Формула медіани трикутника: розуміння і застосування
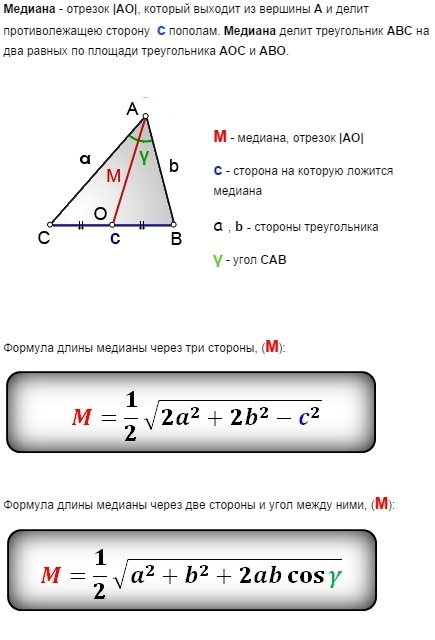
Медіана трикутника — це відрізок, який сполучає вершину трикутника з серединою протилежної сторони, таким чином розбиваючи трикутник на дві рівновеликі частини. Важливим аспектом розв’язування багатьох геометричних задач є вміння коректно використовувати формулу медіани трикутника. Ця формула дозволяє обчислити довжину медіани за відомими сторонами трикутника, що є надзвичайно корисним інструментом при взаємодії з геометричними побудовами та теоріями.
Визначення медіани трикутника
У трикутнику кожна з медіан починається від вершини і проходить через середину протилежної сторони. Таким чином, трикутник має три медіани. Ці медіани перетинаються в одній точці, яка називається центроидом трикутника. Центроид ділить кожну медіану у відношенні 2:1, що є важливою властивістю для геометричних доведень і побудов.
Формула медіани трикутника
Формула медіани трикутника дає можливість визначити довжину медіани, використовуючи сторони трикутника. Нехай ( a ), ( b ), ( c ) — сторони трикутника, а ( m_a ) — медіана, проведена до сторони ( a ). Формула для обчислення медіани ( m_a ) виглядає наступним чином:
[ m_a = sqrt{frac{2b^2 + 2c^2 – a^2}{4}} ]
Це рівняння є основним для розв’язування задач, де потрібно знайти довжину медіани безпосередньо за відомими сторонами трикутника.
Використання формули на практиці
Враховуючи вищеописану формулу, розглянемо приклад її використання для трикутника з відомими сторонами:
- Задача: Дано трикутник зі сторонами ( a = 7 ), ( b = 9 ), ( c = 5 ). Знайти медіану, проведену до сторони ( a ).
- Підставляємо значення сторін у формулу:
[ m_a = sqrt{frac{2 times 9^2 + 2 times 5^2 – 7^2}{4}} ] - Розраховуємо квадрат:
[ m_a = sqrt{frac{2 times 81 + 2 times 25 – 49}{4}} ] - Виконуємо підрахунки:
[ m_a = sqrt{frac{162 + 50 – 49}{4}} = sqrt{frac{163}{4}} = sqrt{40.75} approx 6.38 ]
Таким чином, медіана, проведена до сторони ( a ), становить приблизно 6.38 одиниць довжини.
Таблиця співвідношень для медіан
Ось представлена таблиця, яка допоможе в розрахунках співвідношень для медіан в різних випадках:
| Сторона (( a )) | Сторона (( b )) | Сторона (( c )) | Медіана (( m_a )) |
|---|---|---|---|
| 7 | 9 | 5 | 6.38 |
| 10 | 8 | 6 | 7.5 |
| 12 | 11 | 8 | 8.66 |
Висновок
Формула медіани трикутника є цінним інструментом, що дозволяє значно спростити вирішення багатьох задач у геометрії. Розуміння і вміння правильно використовувати цю формулу може допомогти як студентам, так і досвідченим математичним дослідникам в їх повсякденній практиці. Вивчення вказаних геометричних принципів підсилює математичну інтуїцію та покращує загальні навички аналітичного мислення.