Комбинаторика: Формула для Розрахунків у Ймовірносних Завданнях
Тема комбинаторика формула завжди була однією з найважливіших в області математики та ймовірності. В основі комбінаторики лежать методи та формули, які допомагають визначати різні способи комбінування елементів множини для вирішення практичних задач. У цій статті ми розглянемо основні комбинаторні формули та їх застосування у різних контекстах.
Що таке Комбинаторика?
Комбинаторика — це розділ математики, що займається дослідженням способів упорядкування та розміщення елементів в множині. Основні завдання комбінаторики включають в себе підрахунок кількості можливих конфігурацій, які можуть виникнути при певному розташуванні елементів.
Основні Комбинаторні Формули
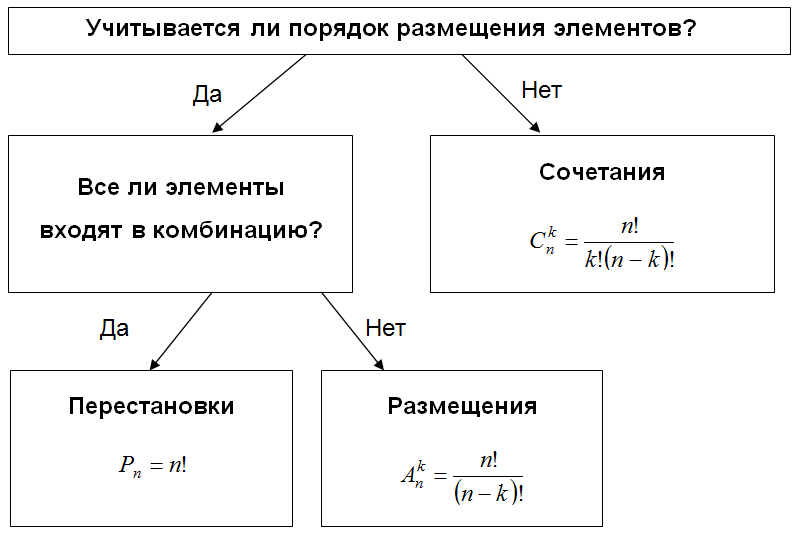
Існує кілька основних формул в комбінаториці, які використовуються для вирішення задач. Розглянемо кожну з них детальніше.
| Формула | Описання |
|---|---|
| Факторіал (n!) | Факторіал числа n – це добуток всіх натуральних чисел від 1 до n. Використовується для підрахунку кількості упорядкованих перестановок. |
| Перестановки (Pn) | Кількість способів упорядкування n елементів. Формула: n!. |
| Розміщення (Ank) | Кількість способів вибрати та упорядкувати k елементів з n. Формула: n! / (n-k)!. |
| Комбінації (Cnk) | Кількість способів вибрати k елементів з n без урахування порядку. Формула: n! / (k!(n-k)!). |
Приклади Використання Комбинаторних Формул
За допомогою комбинаторики можна вирішувати широкий спектр задач – від планування розкладів до аналізу даних у генетичних дослідженнях. Розглянемо деякі приклади найпоширеніших завдань:
- Перестановка з різними елементами: Щоб знайти кількість способів розміщення унікальних елементів, наприклад, скільки різних комбінацій можливе при розташуванні книг на полиці, ми використовуємо формулу перестановок.
- Комбінації у лотереї: При виборі чисел у лотереї важливо підрахувати кількість можливих комбінацій обраних номерів. Тут на допомогу приходить формула комбінацій.
- Розміщення обраних елементів: У спортивних змаганнях часто виникає питання, як вибрати певну кількість учасників з великої кількості за допомогою розміщення.
Застосування Комбинаторних Формул у Житті
Застосування комбинаторика формула не обмежується лише теорією. Вона також знаходить застосування у реальному житті, особливо у галузі інформаційних технологій, статистики, економіки та наукових досліджень.
- Розробка алгоритмів: Застосування комбінаторних структур для оптимізації алгоритмів у програмуванні.
- Захист інформації: Використання криптографії для захисту даних, де комбинаторні формули грають ключову роль у шифруванні інформації.
- Звітність та прогнозування: Статистика та аналіз даних для визначення тенденцій та ймовірностей.