Площа Куба Формула: Все, Що Потрібно Знати
Вступ до Площі Куба та Її Значення
Тема “площа куба формула” є надзвичайно важливою для розуміння багатьох математичних і практичних концепцій. Куб, як одна з основних геометричних фігур, має значну роль у різних галузях наукових досліджень, від архітектури до фізики. Визначення площі його поверхні дозволяє отримати базові відомості про його властивості та характеристики.
Формула Визначення Площі Поверхні Куба
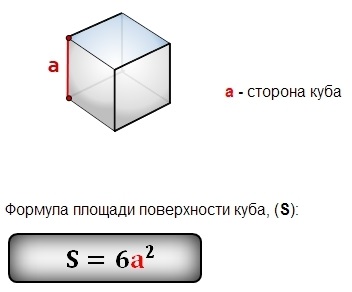
Куб є спеціальним випадком прямокутного паралелепіпеда, всі грані якого є квадратами. Це спрощує обчислення площі поверхні цієї геометричної форми. Формула для визначення площі поверхні куба базується на простій геометричній закономірності:
Площа поверхні куба = 6a2,
де a – довжина ребра куба.
Детальне Описання Формули
Щоб зрозуміти цю формулу детальніше, розгляньмо її складові:
- Куб має 6 квадратних граней.
- Площа однієї грані обчислюється по формулі: a2, де a — довжина грані.
- Оскільки куб має шість таких граней, загальна площа поверхні обчислюється як 6, помножене на площу однієї грані, тобто 6a2.
Практичне Застосування Формули
Формула площі куба широко застосовується в різних галузях, включаючи:
- Будівництво і архітектуру для розрахунку матеріалів.
- Фізику для визначення теплових або електричних характеристик об’єктів.
- Інженерію і дизайн, для створення компактних та функціональних форм.
Приклади Використання Формули в Практичних Завданнях
Розгляньмо кілька прикладів використання формули на практиці, щоб зміцнити розуміння:
Приклад 1: Розрахунок Площі для Геометричних Завдань
Обчислімо площу куба з довжиною ребра 4 метри:
| Операція | Опис | Встановлення |
|---|---|---|
| 1 | Обчислюємо площу однієї грані | a2 = 42 = 16 кв.м |
| 2 | Обчислюємо загальну площу поверхні | 6 * 16 = 96 кв.м |
Приклад 2: Застосування в Реальному Житті
Уявімо, що потрібно пофарбувати кубічну скульптуру в парку, кожна ребро якої має довжину 2 метри. Важливо знати загальну площу для розрахунку кількості фарби:
Площа поверхні = 6 * (22) = 6 * 4 = 24 кв.м
Таким чином, для фарбування потрібної кількості поверхні знадобиться фарба для 24 квадратних метрів.
Висновок
Отже, розуміння та використання “площа куба формула” є критично важливими для різних рішень та інженерних задач. Визначення площі поверхні куба за допомогою простої формули 6a2 дозволяє швидко і точно розраховувати параметри геометричних об’єктів у теорії та практиці.
