Формула площі квадрата: коротке і розгорнуто пояснення
Коли ми говоримо про геометричні фігури, одна з базових і найбільш розповсюджених—це квадрат. Формула площі квадрата є простою і легко застосованою, що робить її основою для розуміння геометричних концепцій. У цьому матеріалі ми розглянемо, як ця формула виглядає, її виведення та застосування.
Що таке квадрат?
Квадрат—це чотирикутник, у якого всі чотири сторони рівні та всі кути прямі (по 90 градусів). Це робить його особливим випадком прямокутника. Простота форми квадрата робить його ідеальним об’єктом для вивчення основних аспектів геометрії, включаючи обчислення площі.
| Елемент | Опис |
|---|---|
| Сторона | Довжина одної сторони квадрата. |
| Кут | 90 градусів. |
Формула площі квадрата
Формула для знаходження площі квадрата—це одне з найпростіших і корисних виражень у геометрії:
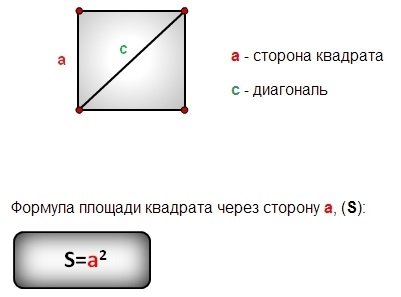
- Позначимо сторону квадрата як a.
- Тоді площа квадрата (S) обчислюється за формулою: S = a².
Це означає, що для знаходження площі квадрата потрібно піднести довжину його сторони до квадрату.
Виведення формули
Давайте розглянемо, як власне виводиться ця формула на простому прикладі:
- Уявімо квадрат зі стороною a.
- Площа—це кількість одиничних квадратів, які можуть поміститися всередині фігури.
- Оскільки квадрат має рівні сторони, у кожному з напрямків примикає a одиничних квадратів.
- Отже, загальна кількість одиничних квадратів дорівнює a × a, або a².
Застосування формули
Використання формули площі квадрата широко застосовується в багатьох математичних і реальних завданнях. Наприклад, у будівництві, архітектурі, дизайні—усюди, де необхідно обчислити площу квадратних поверхонь. Адже, знаючи площу, можна легко дізнатися, скільки матеріалу потрібно для покриття підлоги чи стіни.
Ось ще декілька прикладів:
- Обчислення площі керамічної плитки для підлоги або стін.
- Визначення площі, яку покриває квадратне вікно чи двері.
- Розрахунок площі екрану квадратної форми для різних пристроїв.
Отже, формула площі квадрата відіграє ключову роль у багатьох як теоретичних, так і практичних задачах. Сподіваємося, що це введення допомогло вам зрозуміти, наскільки ця формула проста і в той же час надзвичайно важлива у нашому повсякденному житті.