Формула Площа Круга: Розуміння та Застосування
Формула площа круга є одною з фундаментальних в математиці, яка дозволяє вирахувати площу поверхні, обмеженої окружністю. Знання цієї формули є важливим не лише в математиці, але й в різних науках та інженерних дисциплінах.
Що Таке Коло та Його Властивості
Коло є геометричною фігурою, яка складається з усіх точок на площині, що знаходяться на фіксованій відстані (радіус) від центра кола. Ця проста на перший погляд фігура має чимало важливих властивостей і використовується в різних галузях, таких як фізика, інженерія, астрономія тощо.
Формула площа круга
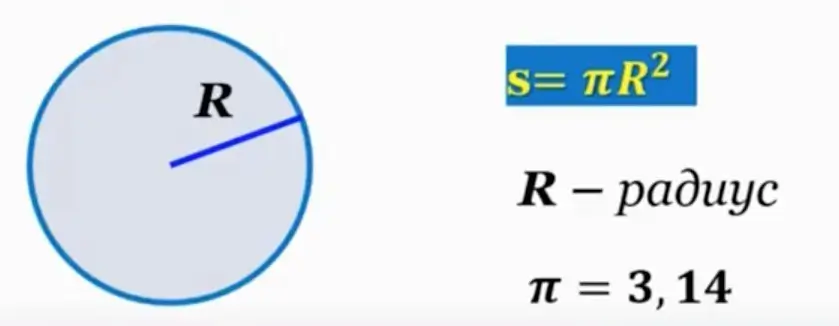
Формула для обчислення площі круга, як відомо, виглядає так:
| Формула | A = πr² |
|---|
Де:
- π – число Пі, яке приблизно дорівнює 3.14159
- r – радіус круга
Ця формула є універсальною і використовується в різних контекстах, коли потрібно визначити площу круга з відомим радіусом.
Як Обчислити Площу Круга: Покрокова Інструкція
- Знайдіть радіус круга. Це відстань від центра круга до будь-якої точки на його межі. Часто радіус відомий з умов завдання, або його потрібно обчислити з інших даних.
- Підставте радіус у формулу. Використовуйте формулу площа круга A = πr², щоб підставити значення радіуса.
- Виконайте множення. Помножте число пі (π) на квадрат радіуса.
- Одержіть результат. Обчислений добуток є площею вашого круга.
Застосування Формули в Практиці
Площа круга знаходить своє використання в багатьох галузях:
- Інженерія: Обчислення площі сегментів у механічних конструкціях або плануванні зон забудови.
- Фізика: Визначення параметрів руху об’єктів по кругових траєкторіях.
- Архітектура: Розрахунок площ в архітектурних проектах з круглими елементами.
Резюме
Формула площа круга є важливим математичним інструментом, який є основою для багатьох прикладних завдань. Її простота і універсальність роблять її незамінною в багатьох сферах, дозволяючи точно і швидко отримати потрібний результат. Розуміння цієї формули та вміння її правильно застосовувати є важливою навичкою для кожного, хто працює з геометричними фігурами.