Формула площі кола: сутність та застосування
Формула площі кола є одним із основних елементів геометрії, яка дозволяє обчислювати площу круга за його радіусом або діаметром. Ця формула часто використовується як в теоретичних, так і в практичних завданнях, пов’язаних із просторовими обчисленнями.
Основи формули площі кола
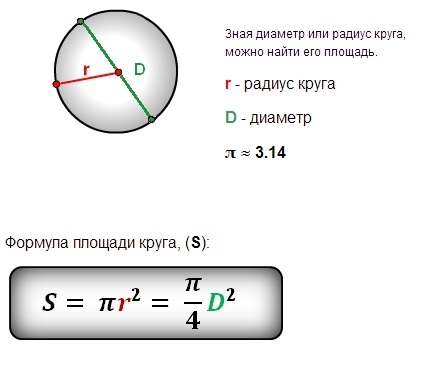
Перш ніж перейти до обчислення площі кола, необхідно зрозуміти, що таке круг і коло. Коло — це замкнута лінія, всі точки якої рівновіддалені від даного центру. Круг — це область, обмежена колом. Формула площі кола визначається через радіус або діаметр круга.
| Позначення | Опис |
|---|---|
| r | Радіус круга |
| d | Діаметр круга (d = 2r) |
| π | Число Пі (π ≈ 3.14159) |
Основна формула площі кола виглядає так:
- S = πr², де S — площа кола.
Якщо відомий діаметр круга, використовують іншу формулу, яка також виводиться з основної:
- S = (πd²) / 4
Застосування формули площі кола
Ця формула надає важливе значення в багатьох галузях, таких як фізика, інженерія, архітектура та інші. Давайте розглянемо деякі конкретні приклади:
- Інженерія: Обчислення площі поверхні деталей машин, наприклад, шківів або підшипників.
- Архітектура: Проєектування куполів, арочних конструкцій та арок.
- Фізика: Визначення площі перерізу циліндричних об’єктів для розрахунку тиску або об’єму.
Приклади розв’язання задач
Розглянемо конкретний приклад для кращого розуміння:
- Задача: Знайти площу круга з радіусом 5 см.
- Розв’язок: Використовуємо формулу S = πr²
- Обчислення: S = π × 5² ≈ 3.14159 × 25 = 78.54 см²
Таким чином, площа кола з радіусом 5 см дорівнює приблизно 78.54 см².
Історичний контекст
Ідея формули площі кола має дуже давнє походження. Математики Стародавньої Греції, такі як Архімед, зробили значний внесок у розуміння цієї теми. Саме Архімед вперше ввів методи обчислення площі круга через вписані багатокутники, що зрештою дозволило дійти до сучасного розуміння числа π та формули площі кола.
Висновок
Формула площі кола є важливим інструментом у геометрії, який застосовується в багатьох наукових і практичних галузях. Знання цієї формули є базовим для кожного, хто вивчає математику чи будь-яку з її суміжних областей, і надає можливість розуміти та застосовувати фундаментальні принципи обчислень площ.