Формула об’єму кулі та її застосування
Формула об’єму кулі займає важливе місце в геометрії та є основою для багатьох інженерних і наукових розрахунків. Вона дозволяє визначити об’єм тривимірної фігури, окресленої рівновіддаленими точками від центру. Обчислення об’єму кулі стали важливою частиною як класичної геометрії, так і сучасних додатків у фізиці та інженерії.
Основи формули
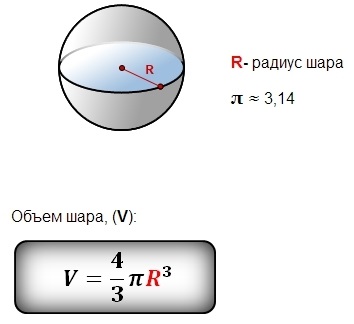
Куля – це геометричне тіло, всі точки якого знаходяться на однаковій відстані від центра. Отже, для розрахунку об’єму кулі використовується наступна формула:
V = (4/3)πr³
де:
- V – об’єм кулі
- π – математична константа пі, приблизне значення 3.14159
- r – радіус кулі
Формула об’єму кулі дозволяє легко визначити об’єм, знаючи лише радіус або діаметр кулі. Важливо зауважити, що точність розрахунків залежить від того, наскільки правильно ви визначите радіус.
Історія і докази
Формула об’єму кулі відома з часів Стародавньої Греції. Архімед перший виявив та довів цю формулу, використовуючи принципи інтеграції, задовго до того, як ця наука була офіційно розроблена. Він встановив, що об’єм кулі дорівнює об’єму трьох рівних конусів з основою, рівною площі великого кола кулі, і висотою, рівною радіусу.
Докази існують і в інших культурах, які спиралися на математичні принципи для знаходження об’єму сферичних об’єктів у практичних додатках, таких як астрономія та будівництво.
Практичне застосування
Формула об’єму кулі застосовується не лише в теоретичних розрахунках, але й у низці прикладних наук:
- Фізика: Вимірювання об’ємів планет і космічних тіл.
- Інженерія: Розрахунки в проєктуванні резервуарів та різних ємностей.
- Біологія: Вивчення клітин і їх об’ємних характеристик.
- Хімія: Визначення об’ємів атомів і молекул у сферичному моделюванні.
Порівняння з іншими геометричними тілами
Формула об’єму кулі може бути порівняна з формулами об’ємів інших тривимірних форм. Нижче наведена таблиця для порівняння:
| Форма | Формула об’єму |
|---|---|
| Куля | V = (4/3)πr³ |
| Куб | V = a³ |
| Циліндр | V = πr²h |
| Конус | V = (1/3)πr²h |
Висновок
Формула об’єму кулі є ключовим інструментом у геометрії та багатьох інших науках. Вона забезпечує можливість точного розрахунку об’єму сферичних форм, що має велике значення для інженерії, фізики, хімії та багатьох інших дисциплін. Знання цієї формули та розуміння її застосування відкривають широкі можливості для вирішення складних задач у різних галузях науки та техніки.