Формула площі повної поверхні циліндра
Формула площі повної поверхні циліндра є важливою математичною концепцією, що знаходить застосування у різних наукових і практичних сферах. В наведеній статті розглянемо детальніше цю формулу, а також основні аспекти, що впливають на розрахунок площі циліндричної поверхні.
Основи геометрії циліндра
Циліндр — це тривимірна фігура, утворена переворотом прямокутника навколо однієї з його сторін. Його основними елементами є:
- Основа: дві рівні круглі площини, котрі розташовані паралельно один до одного.
- Бічна поверхня: поверхня, що з’єднує круги основи.
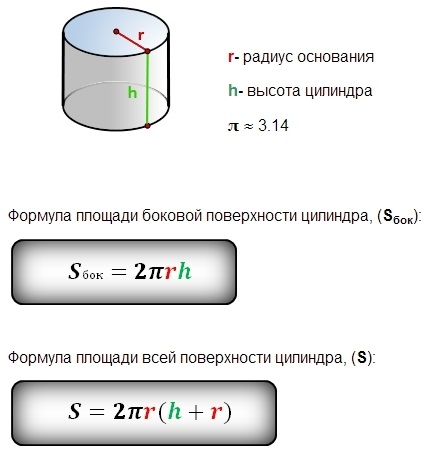
- Висота (h): перпендикулярна відстань між основами.
- Радіус (r): радіус основи циліндра.
Компоненти повної поверхні циліндра
- Площа двох круглих основ: Формула для площі основи одного кругла виглядає як πr². Площу обох основ, відповідно, можна обчислити як 2πr².
- Площа бічної поверхні: Бічна поверхня є прямокутником, довжина якого дорівнює довжині кола основи (2πr), а ширина — висоті циліндра (h). Відповідно, площу бічної поверхні можна обчислити як 2πrh.
Формула площі повної поверхні циліндра
З урахуванням обчислення площі основ і бічної поверхні, формула площі повної поверхні циліндра виглядає наступним чином:
| Формула | Пояснення |
|---|---|
| S = 2πr(h + r) | S — повна площа поверхні, r — радіус основи, h — висота циліндра. |
Ця формула об’єднує площу двох основ і бічної поверхні, утворюючи завершене обчислення для повної поверхні циліндра.
Застосування формули в реальному світі
Формула площі повної поверхні циліндра використовується у багатьох галузях:
- Інженерія: при проектуванні труб, резервуарів або балонів.
- Архітектура: у проектуванні архітектурних елементів, таких як колони.
- Наука: у фізиці та хімії для моделювання циліндричних об’єктів.
Знання формули площі повної поверхні циліндра є корисним інструментом для спеціалістів різних галузей, дозволяючи точно здійснювати обчислення та оптимізувати використання матеріалів.
Підсумки
Формула площі повної поверхні циліндра є критично важливою для розрахунків в різноманітних технічних і наукових дисциплінах. Добре розуміння її компонентів та застосування в реальних ситуаціях відкриває можливості для точнішого використання ресурсів та підвищення ефективності у професійній діяльності.