Довжина кола: формула і застосування
Довжина кола формула — це один із фундаментальних аспектів геометрії, який вивчається у школах і використовується у багатьох прикладних галузях від архітектури до фізики. Розуміння цієї теми має важливе значення для розв’язання задач, пов’язаних із колами, а також для розвитку критичного мислення в процесі вивчення математики.
Основи геометрії кола
Коло — це множина всіх точок на площині, віддалених на однакову відстань від центру. Ця відстань називається радіусом, а сам центр — центром кола. Довжина кола, або периметр, — це відстань, яку можна відміряти по лінії, що утворює коло.
Виведення формули довжини кола
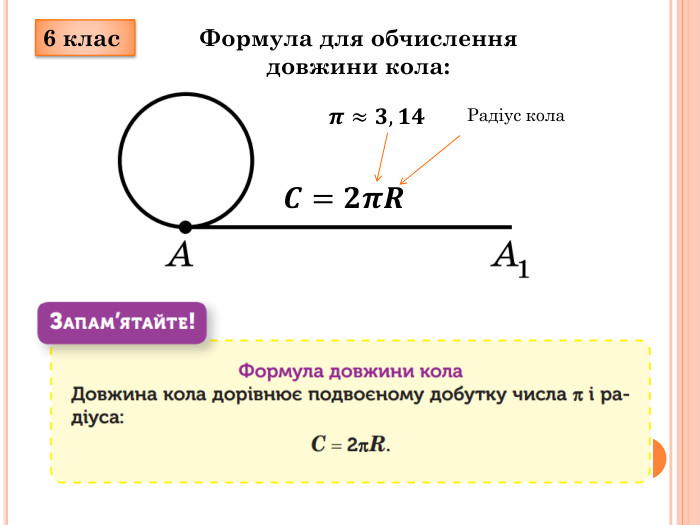
Довжина кола формула має вигляд:
| Співвідношення | Опис |
|---|---|
| C = 2πr | Довжина кола (C) дорівнює добутку чисел 2, π (пі) та радіуса кола (r). |
| C = πd | Довжина кола може бути обчислена як добуток числа π та діаметра кола (d). |
Де π (пі) — це математична константа, приблизно рівна 3.14159.
Практичне застосування
- Будівництво: Архітектори використовують формулу для розрахунку матеріалів, необхідних для спорудження круглих структур, таких як колони.
- Машинобудування: Інженери застосовують цю формулу для креслення деталей машин, де потрібна точність у вимірюваннях кільцювих деталей.
- Щоденне життя: Визначення довжини або обводу таких речей, як капелюхи, колеса або кільця, де потрібна точність.
Висновки
Розуміння, як використовується формула довжини кола, є важливим навиком не лише в науці, але і в повсякденному житті. Цей простий, але ефективний математичний інструмент допомагає візуалізувати й точно визначати багато аспектів фізичного світу. Довжина кола формула служить прикладом того, як абстрактні математичні концепції мають практичне застосування.