Теорема синусів: формулювання та застосування
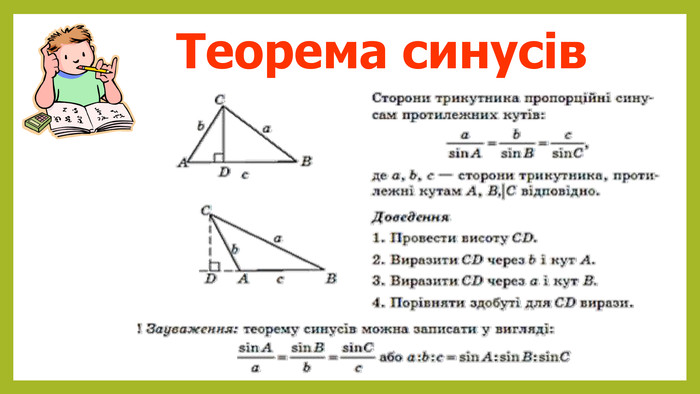
Теорема синусів формулюється так: у будь-якому трикутнику відношення довжини сторони до синуса протилежного кута дорівнює діаметру описаного навколо цього трикутника кола. Ця фундаментальна теорема є важливою частиною тригонометрії, що пропонує ефективні інструменти для розв’язання низки задач, пов’язаних з вимірюванням кутів та сторін трикутників.
Формулювання теореми синусів
Теорема синусів формулюється так:
| Формула |
|---|
| a/sin(α) = b/sin(β) = c/sin(γ) = 2R |
- a, b, c — довжини сторін трикутника
- α, β, γ — протилежні їм кути
- R — радіус описаного кола навколо трикутника
Застосування теореми синусів
Теорема синусів є потужним інструментом для розв’язання задач, пов’язаних із трикутниками, особливо в таких випадках:
- Коли дані дві сторони та кут між ними
- Коли відомо дві сторони і один з протилежних кутів
- Для визначення радіуса описаного кола
- При розв’язанні задач у сферичній геометрії
Приклади практичного використання
Однією з найбільш практичних ситуацій для використання теореми синусів є обчислення третіх елементів, тобто, коли відомі два кути і одна сторона або дві сторони і один кут. Наприклад, при навігації, картографії та геодезії часто потрібні точні вимірювання, де теорема синусів може бути корисною для визначення відстаней та кутів.
Крім того, теорема синусів знаходить застосування в інженерії, архітектурі та навіть у фізиці, де часом важливо розраховувати точні значення кутів між різними компонентами систем.
Переваги використання теореми синусів
Серед основних переваг теореми синусів можна виділити:
- Дозволяє обчислювати значення кутів і сторін, не застосовуючи координати
- Забезпечує альтернативний підхід порівняно з теоремою косинусів
- Легко інтегрується в комплексні геометричні вирішення
Для підрахунку значень безпосередньо через цю теорему, часто необхідно заручитися знанням радіуса описаного кола. Це обмеження можна обійти, звернувшись до інших відомих співвідношень у геометрії, таких як формули Герона для обчислення площі трикутника.
Висновок
Таким чином, теорема синусів є не лише важливим теоретичним досягненням у математичній науці, а й практичним інструментом, що знаходить широке застосування у різних галузях. Її універсальність та простота роблять цю теорему незамінною для багатьох практичних задач. Розуміння її основних концепцій та формулювань сприяє більш ефективному і точному вирішенню складних геометричних питань.