Теорема синусів і косинусів: фундаментальні поняття тригонометрії
Теорема синусів і косинусів відіграють важливу роль у вивченні геометрії та тригонометрії, оскільки саме вони відкривають можливість порівняння сторін і кутів в трикутниках. Ці теореми є основою для вирішення безлічі задач у планіметрії, аналітичній геометрії, фізиці та інших науках.
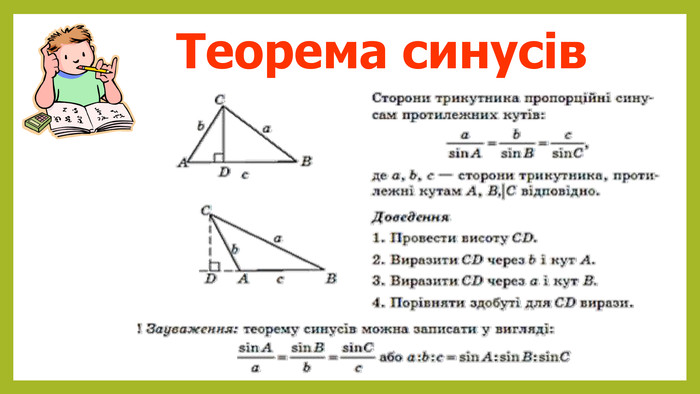
Теорема синусів: співвідношення в трикутнику
Теорема синусів дає можливість знайти відношення між сторонами ненажорного трикутника та їх синусів відповідних кутів. Вона може бути формулювана наступним чином:
- Формула: (< frac{a}{sin A} = frac{b}{sin B} = frac{c}{sin C} = 2R )
- Де (a), (b), (c) – сторони трикутника,
- (A), (B), (C) – протилежні кути,
- (R) – радіус описаного кола навколо трикутника.
Теорема синусів є особливо корисною при роботі з неамбулами (неправильними) трикутниками, де відомі два кути і одна сторона або дві сторони і непов’язані кути. Застосування теореми синусів дозволяє обчислити невідомі елементи трикутника з високою точністю.
Теорема косинусів: загальне розв’язання трикутника
На відміну від теореми синусів, теорема косинусів забезпечує спосіб визначення третьої сторони будь-якого трикутника та її відношення до кутів. Вона формулюється так:
- Формула: (
c^2 = a^2 + b^2 – 2ab cdot cos C ) - де (cos C) – косинус протилежного кута (C).
Таким чином, теорема косинусів є узагальненням теореми Піфагора для довільного трикутника. Якщо кут (C) є прямим, тоді теорема косинусів спрощується до теореми Піфагора, де (cos 90° = 0).
Застосування теорем синусів і косинусів
Теореми для трикутників мають ключове значення у різних галузях науки і технологій:
- Астрономія: Точний розрахунок відстаней між небесними тілами.
- Інженерія: Визначення структурних сил та стійкості конструкцій.
- Геодезія: Вимірювання земельних ділянок та визначення їх координат.
- Фізика: Аналіз коливальних і хвильових процесів.
Порівняльна таблиця основних положень теорем
| Параметр | Теорема синусів | Теорема косинусів |
|---|---|---|
| Застосування | Усі типи трикутників | Довільні трикутники |
| Елементи | Сторони та протилежні кути | Сторони та будь-які кути |
| Тип трикутника | Гострокутні, тупокутні | Гострокутні, тупокутні, прямокутні |
Таким чином, теорема синусів і косинусів забезпечують потужний інструмент для розв’язання трикутників і розуміння співвідношень в геометрії. Вони є основою для багатьох арифметичних і аналітичних методів, що використовуються в технічних та наукових дослідженнях.