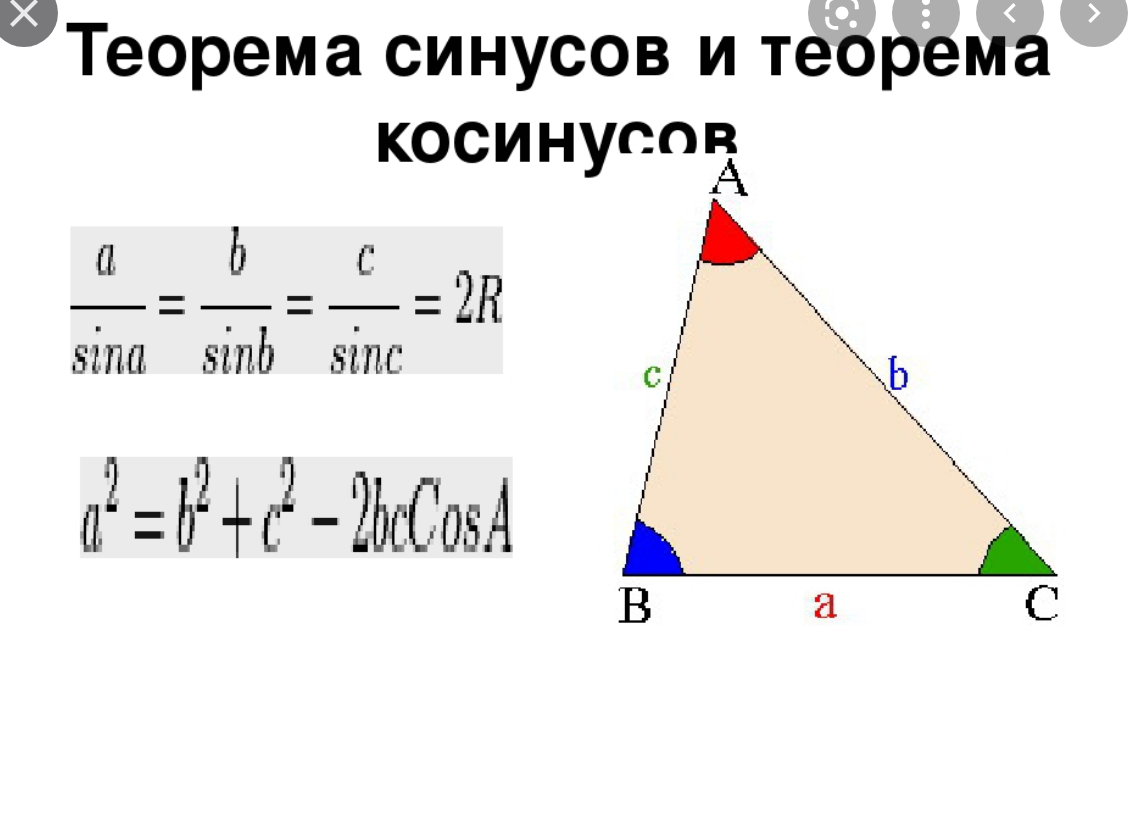
Теорема синуса: Детальний розбір і застосування
Ключове твердження у тригонометрії, яке відоме як теорема синуса, забезпечує зв’язок між довжинами сторін трикутника і синусами його кутів. Розглянемо глибше суть цієї теореми, її значення та застосування в різних математичних і практичних задачах.
Формулювання теореми синуса
Укладаючи сутність теореми, скажемо, що вона описує співвідношення між сторонами трикутника і протилежними їм кутами. Теорема стверджує, що для довільного трикутника ABC:
- Формула:
(a/sin(α)) = (b/sin(β)) = (c/sin(γ))
| Елемент | Опис |
|---|---|
| a, b, c | Довжини сторін трикутника ABC |
| α, β, γ | Кути протилежні відповідно сторонам a, b, c |
Доказ теореми синуса
Розглянемо основний підхід до доведення теореми синуса за допомогою вписаного кола.
- Розглянемо трикутник ABC і вписане коло з центром O.
- Відрізок OM перпендикулярний до сторони BC, де M — точка дотику кола.
- Утворюємо вираз для синуса кожного кута, використовуючи відрізки кола:
- Сторона a протилежна куту α, отже OM = R·sin(α).
- Аналогічно для сторін b і c: R·sin(β) і R·sin(γ) відповідно.
- Відповідно, рівність (a/sin(α)) = (b/sin(β)) = (c/sin(γ)) = 2R доводить формулу теореми.
Застосування теореми синуса
Теорема синуса є не лише теоретично важливою, але й широко використовуваною в ряді практичних задач:
- Геодезія: Визначення відстаней та кутів на місцевості при вимірюванні важкодоступних ділянок.
- Астрономія: У розрахунках міжзоряних відстаней та орбіт.
- Інженерія: При проектуванні конструкцій, де потрібні вірні розрахунки геометричних характеристик.
Висновок
Таким чином, теорема синуса є надзвичайно універсальним інструментом у математиці та інженерійному аналізі. Її здатність об’єднувати геометричні та тригонометричні властивості трикутників дозволяє ефективно розв’язувати задачі, які потребують точності й грунтовних знань.