Теорема Котельникова: Основи та застосуання
Теорема Котельникова є фундаментальною концепцією в області цифрової обробки сигналів, яка має ключове значення для розуміння процесу перетворення аналогових сигналів у цифрову форму. Вона була сформульована російським вченим В. А. Котельниковим у 1933 році, відкривши новий підхід до таких процесів, як передача та обробка даних.
Історичний контекст
В ті часи, коли аналогові технології домінували у світі, питання про запам’ятовування, передавання та обробку інформації саме в цифровому вигляді було досить новаторським. Котельников запропонував метод, що дозволяв переводити неперервний аналоговий сигнал у дискретний набір даних без втрати інформації. Це відкрило шлях до розвитку цифрових технологій, які стали невід’ємною частиною сучасного світу.
Суть теореми Котельникова
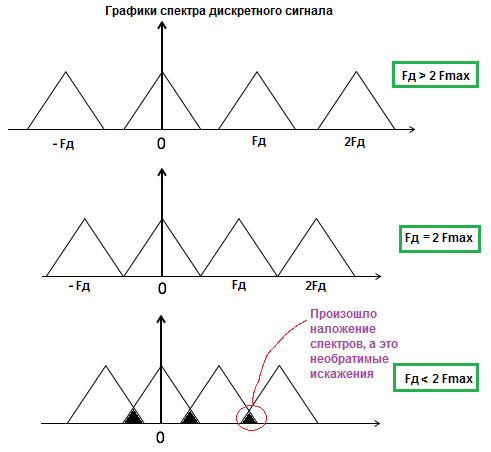
Теорема Котельникова, також відома як теорема відбору або теорема дискретизації, стверджує: для того, щоб повністю відновити аналоговий сигнал з його дискретних значень, частота дискретизації повинна бути як мінімум удвічі більшою за максимальну частоту оригінального сигналу. Це означає, що сигнал, що має максимальну частоту Fmax, може бути точно відтворений, якщо його частота дискретизації перевищує 2Fmax.
Практичне застосування
- Аудіо та відео технології: Одним з найвідоміших застосувань теореми є запис та відтворення звуку в аудіо системах, де для відтворення якісного звуку частота дискретизації вибирається на рівні 44.1 кГц.
- Телекомунікації: У галузі передачі даних та комунікацій використовується для забезпечення надійності та точності переданих сигналів.
- Обробка зображень: Теорема застосовується також для обробки зображень, особливо при розгляді частотних компонентів зображення.
Таблиця частот дискретизації
| Тип сигналу | Частота дискретизації (Гц) |
|---|---|
| Аудіо CD | 44,100 |
| Телебачення | 24,000 |
| Медичні зображення | 48,000 |
Проблеми та виклики
Попри свою простоту, теорема Котельникова несе з собою ряд викликів:
- Аліасинг: Якщо частота дискретизації менша за подвійний показник максимальних частот оригінального сигналу, відбувається перекриття, що призводить до викривлення.
- Обмеження реконструкції: На практиці ідеальна реконструкція зазвичай обмежена через шум та перешкоди.
- Витрати ресурсів: Чим вища частота дискретизації, тим більше обчислювальних ресурсів необхідно для обробки даних.
Висновок
Теорема Котельникова є основою сучасних цифрових систем, забезпечуючи можливість ефективного перетворення та обробки сигналів. Її принципи залишаються важливими для різноманітних застосувань як в науковій, так і в прикладній сферах. Завдяки цьому, розуміння та правильне застосування теореми є ключовим для успішної роботи як з аудіо-візуальними, так і іншими даними.