Формула об’єму куба: основи, приклади, застосування
Формула об’єму куба часто використовується в геометрії для обчислення простору, який займає ця геометрична фігура. Куб є тривимірною фігурою з рівними за довжиною сторонами, тому обчислення його об’єму є доволі простим завданням для математиків і студентів.
Базове розуміння формули
Куб є особливим випадком прямокутного паралелепіпеда, оскільки всі його ребра рівні. Це спрощує процес обчислення його об’єму. Форма куба робить його унікальним з точки зору симетрії, оскільки всі його площини та кути рівні.
Формула об’єму куба
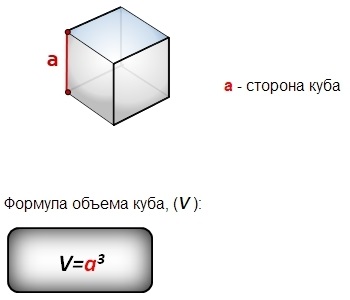
Об’єм куба можна знайти, використовуючи формулу:
| Формула | Пояснення |
|---|---|
| V = a3 | Де V – об’єм куба, а a – довжина сторони куба. |
Це означає, що для обчислення об’єму куба достатньо піднести довжину його сторони до третьої степені.
Приклад обчислення
Розглянемо приклад, щоб краще зрозуміти, як працює формула об’єму куба:
- Припустімо, що довжина сторони куба дорівнює 4 см.
- Використовуємо формулу: V = 43.
- Обчислюємо: V = 4 × 4 × 4 = 64.
- Таким чином, об’єм куба дорівнює 64 кубічних сантиметри.
Застосування об’єму куба в реальному світі
- Упаковка та логістика: Знання об’єму куба допомагає ефективно використовувати простір при транспортуванні товарів і їх зберіганні.
- Будівництво та архітектура: Практично в кожному проекті будівництва виникає необхідність обчислення об’ємів для зміцнення структур або розрахунку кількості матеріалів.
- Екологія та наука: Багато наукових досліджень вимагають точних обчислень об’ємів для моделювання процесів у природному середовищі.
Висновок
Формула об’єму куба є зрозумілим, але важливим інструментом в багатьох галузях. Вона дає змогу швидко й ефективно переходити від абстрактних математичних понять до реальних, практичних застосувань. Вміння обчислювати об’єм куба є незамінним не лише для студентів математики, але і для професіоналів в різних галузях інженерії, науки та економіки.