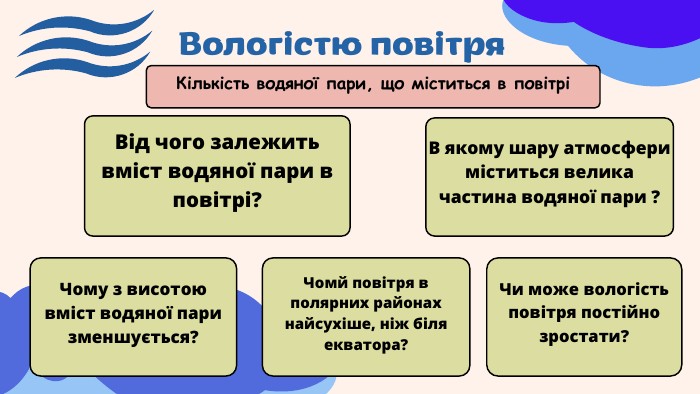
Обернена теорема Вієта: Загальний огляд і практичне застосування
Обернена теорема Вієта відіграє важливу роль у математичному аналізі, особливо у вивченні властивостей квадратних рівнянь. Ця теорема дозволяє перейти від коренів рівняння до його коефіцієнтів. Таке знання є ключовим у розв’язанні багатьох алгебраїчних задач.
Теорема Вієта: Основи
Щоб зрозуміти обернену теорему Вієта, важливо спочатку розглянути основну теорему Вієта. Для квадратного рівняння:
ax² + bx + c = 0,
де a, b, і c — коефіцієнти, теорема Вієта встановлює зв’язок між коренями x₁ і x₂ та коефіцієнтами рівняння:
- Сума коренів: x₁ + x₂ = -b/a
- Добуток коренів: x₁ * x₂ = c/a
Обернена теорема Вієта
Обернена теорема Вієта працює у зворотному порядку: відомі корені дозволяють знаходити коефіцієнти квадратного рівняння. Вона стверджує, що якщо є числа x₁ і x₂, які задовольняють умовам:
- S = x₁ + x₂
- P = x₁ * x₂
то квадратне рівняння буде мати вигляд:
x² - Sx + P = 0
Вивід оберненої теореми Вієта
Розглянемо, як отримуються коефіцієнти a, b, і c з коренів x₁ і x₂. Як відомо з теореми Вієта для загального рівняння ax² + bx + c = 0:
- Обчислюється сума S: S = x₁ + x₂ = -b/a
- Обчислюється добуток P: P = x₁ * x₂ = c/a
Звідси бачимо, що для рівняння виду x² + bx + c = 0, коефіцієнти будуть:
| Коефіцієнт | Значення |
|---|---|
| b | -S |
| c | P |
Практичне застосування
Обернена теорема Вієта може бути використана для розв’язання різноманітних алгебраїчних та геометричних задач, коли необхідно знаходити рівняння за заданими коренями. Це може бути корисним у таких випадках:
- Визначення геометричних фігур, заданих відносинами між вершинами.
- Оптимізація параметрів в задачах економічного моделювання.
- Побудова рівнянь для моделювання реальних фізичних процесів.
Зокрема, в задачах на побудову графіків функцій обернена теорема Вієта допомагає швидко знайти рівняння параболи, якщо відомі точки перетину цієї параболи з віссю абсцис.
Висновок
Обернена теорема Вієта є невід’ємною частиною арсеналу математика, забезпечуючи зручний метод переходу від коренів квадратного рівняння до його коефіцієнтів. Ця теорема не лише поглиблює наше розуміння алгебраїчних рівнянь, але й надає практичні інструменти для вирішення реальних проблем у різних галузях науки і техніки.