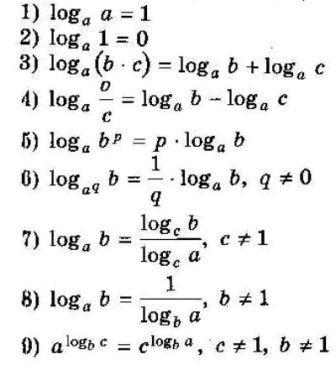Логарифм Формула: Вивчення і Застосування
Логарифм формула є важливим інструментом в математиці, який використовується для розв’язання різноманітних проблем, що стосуються експоненційних залежностей. Використання логарифмів охоплює безліч галузей, від фізики до економіки. У цій статті ми зосередимося на понятті логарифмів, формулі їх обчислення, правилах і прикладах застосування.
Основи Логарифмів
Логарифм числа визначається як показник ступеня, у який потрібно піднести базу логарифма, щоб отримати це число. Формально це записується так:
- logb(a) = c, де bc = a.
У цьому записі:
- b – база логарифма;
- a – число, логарифм якого обчислюється;
- c – логарифм числа a за основою b.
Формули Логарифмів
| Формула | Опис |
|---|---|
| logb(xy) = logb(x) + logb(y) | Логарифм добутку чисел дорівнює сумі логарифмів цих чисел. |
| logb(x/y) = logb(x) – logb(y) | Логарифм частки чисел дорівнює різниці логарифмів чисел. |
| logb(xp) = p*logb(x) | Показник степеню можна винести перед логарифмом як множник. |
| logb(1) = 0 | Логарифм одиниці за будь-якою основою дорівнює нулеві. |
Застосування Логарифмів
Логарифм формула широко застосовується в науці і техніці. Ось декілька прикладів:
- В математиці: Обчислення складних експоненційних рівнянь часто спрощується за допомогою логарифмів.
- У фізиці: Логарифми використовуються для вимірювання рівнів звуку (децибели) та землетрусів (шкала Ріхтера).
- В економіці: Логарифми дозволяють моделювати експоненційне зростання, наприклад, відсотки і капіталовкладення.
Завдяки своїй властивості переводити експоненційні рівняння у лінійні, логарифми значно полегшують розв’язок багатьох реальних завдань.
Таким чином, розуміння логарифмів і вміння користуватися їх формулами є критично важливим для успішного розв’язання математичних задач і аналізу даних у різних галузях науки та техніки.