Формула висоти трикутника: основа геометричних знань
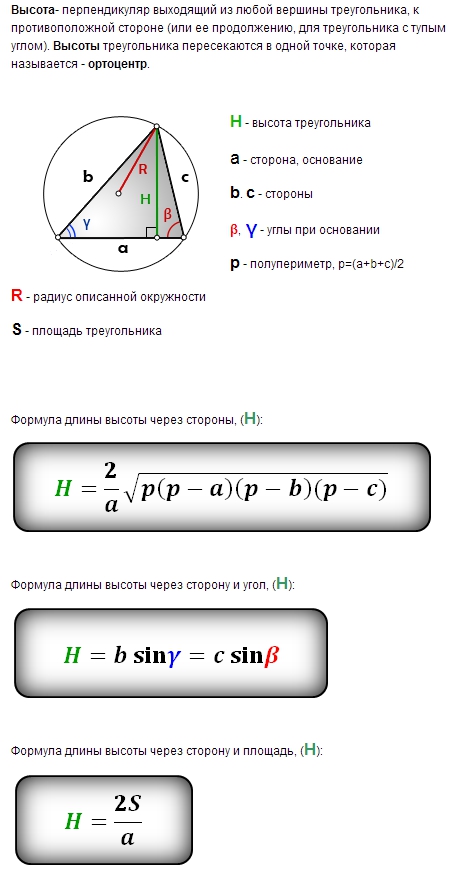
Формула висоти трикутника є фундаментальним елементом у вивченні геометрії, адже вона дозволяє обчислити вертикальну відстань від вершини трикутника до його основи. Визначення висоти трикутника є ключовим у вирішенні багатьох геометричних задач та практичних завдань. На основі класичних геометричних принципів, що включають застосування алгебраїчних та тригонометричних методів, ця формула забезпечує точність розрахунків та дає змогу зрозуміти характеристики різних типів трикутників.
Що таке висота трикутника?
У загальному розумінні, висота трикутника – це перпендикуляр, опущений з вершини трикутника до прямої, яка містить протилежну сторону. Ця сторона називається основою трикутника. Трикутник може мати три висоти, кожна з яких відповідає одній з його сторін.
Формула висоти трикутника
Кожен трикутник має свої особливості, тому формула висоти трикутника може варіюватися залежно від типу трикутника: рівнобедреного, рівностороннього або прямокутного. Проте є універсальна формула для обчислення висоти в будь-якому трикутнику, що ґрунтується на площі трикутника.
Формула, яка виражає це, виглядає наступним чином:
| Тип трикутника | Формула висоти |
|---|---|
| Загальний трикутник | h = (2 * S) / a |
Тут:
- h — висота трикутника, що опущена на сторону a;
- S — площа трикутника;
- a — довжина основи.
Обчислення висоти у спеціальних випадках
Рівносторонній трикутник
Для рівностороннього трикутника, де всі сторони рівні, застосовується спеціальна формула:
h = (a√3) / 2
Де a — довжина сторони трикутника.
Рівнобедрений трикутник
У випадку рівнобедреного трикутника, висота може бути знайдена, використовуючи теорему Піфагора. Якщо a — основа рівнобедреного трикутника та b — його рівні сторони, висота буде дорівнювати:
h = √(b² – (a/2)²)
Прямокутний трикутник
У прямокутному трикутнику висота може бути обчислена безпосередньо як катет, якщо основа – це другий катет. Проте, якщо основа – гіпотенуза, застосовуйте формулу площі для обчислення висоти:
- Гіпотенуза — c;
- Площа — S.
Формула для висоти стане: h = (2 * S) / c.
Застосування формули в реальному житті
Розуміння формули висоти трикутника має безліч практичних застосувань. В геодезії, архітектурі і навіть в авіації, знання як точно обчислити висоту є критично важливим. Від реконструкції історичних будівель до розрахунку оптимального кута для нахилу криш в електричних мережах — ці обчислення забезпечують точність і ефективність.
Висновок
Оволодіння такими базовими концепціями, як формула висоти трикутника, є важливим не тільки для академічних цілей. Це знання також має величезне значення у застосуванні до реальних світових проблем. Використання цих знань дозволяє не лише знайти точні рішення, але й сприяє кращому розумінню функціонування оточуючого світу.