Формула радіуса кола: Розкриття математичного поняття
Формула радіуса кола є одним із фундаментальних понять у геометрії, яке має широке застосування в різних галузях науки та інженерії. Радіус кола визначає основні властивості кола і слугує базою для подальших розрахунків.
Основи визначення радіуса кола
В геометрії коло визначається як множина всіх точок, рівновіддалених від однієї центральної точки. Ця відстань є радіусом кола (R), яка виступає важливим аспектом при визначенні параметрів кола.
Формула радіуса кола відображає зв’язок між радіусом, діаметром (D), та площею (A) кола:
- Відрізок діаметра:
R = D / 2 - З площею кола:
R = √(A / π)
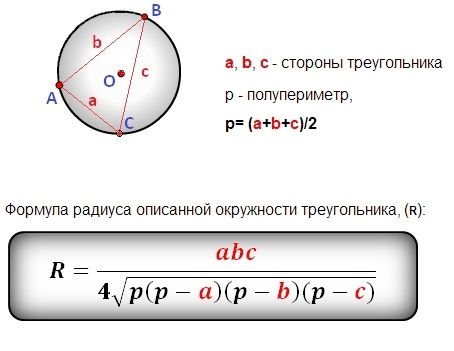
Формула радіуса описаного кола трикутника
У випадку трикутників радіус описаного кола рахується більш складно. Для трикутника зі сторонами a, b, c та площею S формула для обчислення радіуса описаного кола виглядає так:
- Обчисліть півпериметр (p):
p = (a + b + c) / 2 - Використовуйте формулу Герона для обчислення площі:
S = √(p * (p - a) * (p - b) * (p - c)) - Обчисліть радіус описаного кола:
R = (a * b * c) / (4 * S)
Значення для різних типів трикутників
Важливо зазначити, що радіус описаного кола трикутника не є універсальним значенням і змінюється в залежності від типу трикутника:
- Рівносторонній трикутник:
R = a / √3 - Рівнобедрений трикутник: Формула не змінюється, але значення може бути простішим для конкретних випадків.
- Прямокутний трикутник:
R = c / 2(де c — гіпотенуза)
Таблиця значень для практичного застосування
| Тип трикутника | Формула радіуса описаного кола |
|---|---|
| Рівносторонній | R = a / √3 |
| Прямокутний | R = c / 2 |
| Рівнобедрений | Універсальна формула з урахуванням конкретних сторін |
Висновок
Формула радіуса кола є основним інструментом для вивчення властивостей геометричних фігур. Знання формули та її застосування сприяють глибшому розумінню геометрії, а також допомагають вирішувати складні задачі не лише в математичних обчисленнях, але і в практичних застосуваннях. Незалежно від типу трикутника, формула радіуса описаного кола зберігає свою важливість і дозволяє розрахувати параметри з високою точністю.