Формула приведения: основи застосування та приклади
Формула приведения є важливим інструментом в області тригонометрії, який дозволяє спростити та уніфікувати обчислення тригонометричних функцій для різних кутів. Завдяки цій формулі можливо перетворювати значення тригонометричних функцій, які виходять за рамки звичних кутів, до більш зручних і звичних значень.
Що таке формула приведения?
Формула приведения є математичним виразом, що використовується для полегшення обчислень тригонометричних функцій. В основі цих формул лежить ідея, що значення тригонометричних функцій не змінюються незалежно від періодичних обертів або переходів через окремі порівняльні точки, такі як 90°, 180°, 270° та 360°.
Формули приведения: основні принципи
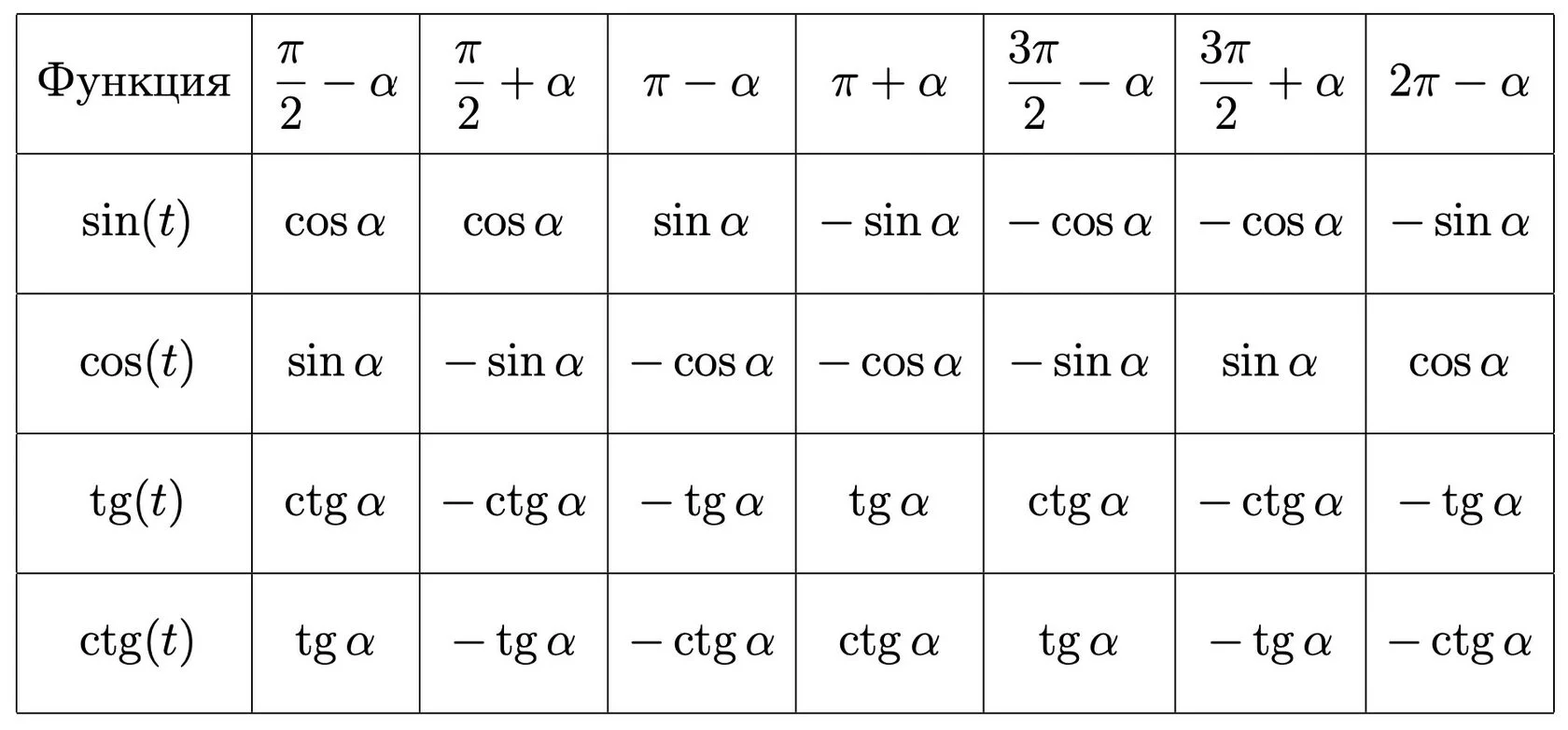
Основний принцип формул приведения полягає в тому, що значення тригонометричних функцій залежить від квадранту, в якому знаходиться кут. Давайте розглянемо основні формули приведения для синуса, косинуса та тангенса:
- Синус (sin):
- sin(180° – α) = sin(α)
- sin(180° + α) = -sin(α)
- sin(360° – α) = -sin(α)
- Косинус (cos):
- cos(180° – α) = -cos(α)
- cos(180° + α) = -cos(α)
- cos(360° – α) = cos(α)
- Тангенс (tan):
- tan(180° – α) = -tan(α)
- tan(180° + α) = tan(α)
- tan(360° – α) = -tan(α)
Застосування формул приведения
Формули приведения використовуються в різних задачах, що передбачають обчислення тригонометричних функцій для нетипових кутів. Це особливо актуально в розв’язанні задач фізики, геодезії, механіки, астрономії та інших наук.
| Функція | Перетворення | Приклад обчислення |
|---|---|---|
| sin(210°) | sin(180° + 30°) = -sin(30°) | -0.5 |
| cos(330°) | cos(360° – 30°) = cos(30°) | 0.866 |
| tan(135°) | tan(180° – 45°) = -tan(45°) | -1 |
Висновки
Використання формул приведения стало важливою частиною вивчення і застосування тригонометричних функцій. Вони допомагають спростити обчислення, зекономити час і зусилля, а також унеможливлюють виникнення помилок під час перетворень. У кінцевому результаті формула приведения слугує надійним інструментом при розв’язанні складних математичних проблем.
Для подальшого вивчення варто відвідати ресурс Sigma Center, що надає додаткову інформацію про різні аспекти формул приведения.