Формула площі ромба: Від теорії до практики
Формула площі ромба є незамінним інструментом для ефективного розв’язання задач у геометрії. Ромб – це чотирикутник, в якому всі сторони рівні, а протилежні кути рівні. Це засадничо спрощує процес обчислень. Але як точно знайти площу цього правильного чотирикутника?
Розуміння властивостей ромба
Ромб має декілька ключових властивостей, які є важливими для обчислення його площі:
- Сторони: Усі чотири сторони ромба рівні.
- Діагоналі: Діагоналі ромба перетинаються під прямим кутом, взаємно поділяючи одна одну на половини.
- Кути: Сума внутрішніх кутів ромба дорівнює 360 градусам.
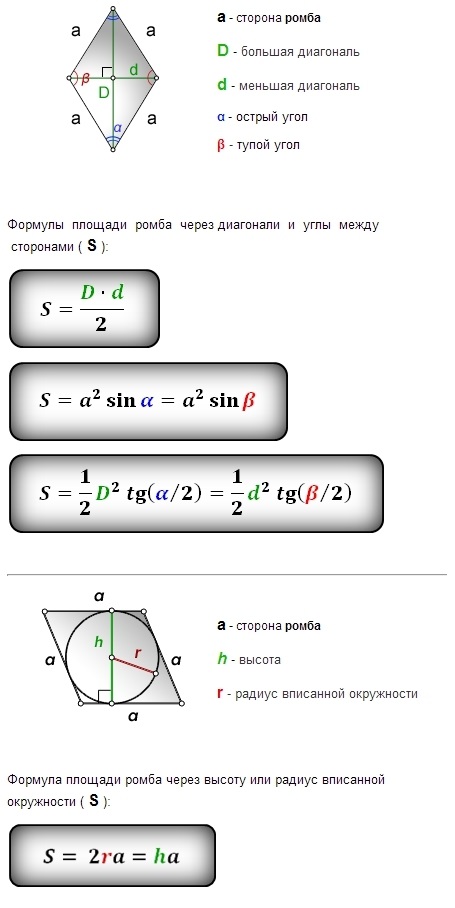
Формула площі ромба
Існують різні підходи до обчислення площі ромба, але найбільш відомою є формула, заснована на його діагоналях:
Формула площі ромба: Якщо d_1 і d_2 – діагоналі ромба, то площу S можна знайти за формулою:
| Формула | Пояснення |
|---|---|
| S = (d_1 × d_2) / 2 | Площа ромба дорівнює половині добутку його діагоналей. |
Альтернативні методи обчислення площі
Хоча площа ромба зазвичай обчислюється за допомогою діагоналей, існують і інші методи:
- Через сторону і висоту: Якщо нам відома довжина сторони a і висота h, що проведена до цієї сторони, то площа S буде:
- Через синус кута: Якщо відома довжина сторони a і один із кутів, то можна застосувати тригонометричну формулу:
S = a × h
S = a² × sin(α)
Практичні приклади
Розглянемо кілька конкретних прикладів оволодіння формулою площі ромба:
- Якщо діагоналі ромба дорівнюють 8 см та 6 см, то площа ромба буде:
- У випадку, коли довжина сторони дорівнює 5 см, а висота 4 см:
S = (8 × 6) / 2 = 24 см²
S = 5 × 4 = 20 см²
Висновки
Формула площі ромба надає нам ефективний спосіб обчислення площі цього геометричного фігура, що може бути корисним у багатьох контекстах. За рахунок особливостей ромба, такі обчислення стають відносно простими і легкодоступними. Запам’ятавши кілька ключових формул, ви будете в змозі розв’язувати як стандартні, так і більш складні задачі, пов’язані з ромбами.