Формула площі рівностороннього трикутника
Одним із класичних завдань в геометрії є обчислення площі трикутника. Формула площі рівностороннього трикутника — це ключове поняття, яке дозволяє знайти площу такого трикутника, знаючи лише одну його сторону. В цьому тексті ми розглянемо, що саме стоїть за цією формулою, чому вона працює і як її застосувати на практиці.
Що таке рівносторонній трикутник?
Перш ніж заглиблюватися в обчислювальні аспекти, варто зрозуміти, що рівносторонній трикутник — це такий трикутник, у якому всі три сторони рівні між собою, а також всі три внутрішні кути дорівнюють 60 градусів. Через такі характеристики, рівносторонній трикутник має низку цікавих властивостей, які полегшують обчислення його площі.
Формула площі рівностороннього трикутника: виведення та пояснення
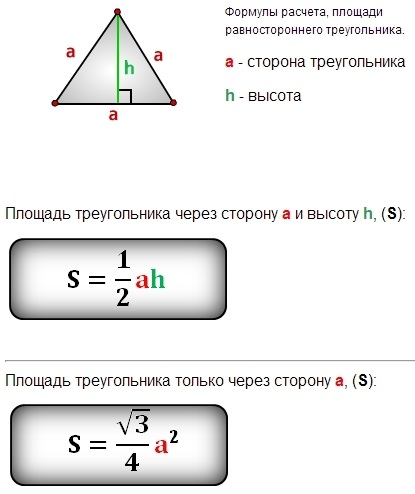
- Формула площі рівностороннього трикутника виглядає наступним чином: S = (a²√3) / 4, де a — довжина сторони трикутника.
- Виведення цієї формули базується на використанні властивостей рівностороннього трикутника та тригонометрії.
- Якщо провести висоту з будь-якої вершини трикутника, то вона ділитиме його на два рівнобедрених прямокутних трикутника. Висота h дорівнює h = a√3/2.
Знайдемо площу за формулою, де h виступає висотою. Площа трикутника знаходиться через відомий вираз S = 1/2 * a * h.
- Підставимо висоту в формулу: S = 1/2 * a * (a√3/2)
- Спрощення дає нам: S = (a²√3) / 4.
Це й є формула площі рівностороннього трикутника, яка свідчить про те, що для обчислення площі достатньо знати лише одну сторону.
Практичне застосування формули
| Довжина сторони (a) | Площа (S) |
|---|---|
| 2 см | √3 см² |
| 5 см | 25√3/4 см² |
| 10 см | 100√3/4 см² |
Залежно від задачі рівносторонній трикутник може стати частиною більш складних геометричних конструкцій. Освоївши формулу площі рівностороннього трикутника, можна ефективніше вирішувати широкий спектр задач.
Основні переваги та особливості формули
Формула площі рівностороннього трикутника є ефективним інструментом в геометрії завдяки своїй простоті та універсальності. Знання цієї формули дозволяє швидко та точно виконувати розрахунки в різноманітних задачах, пов’язаних з рівносторонніми трикутниками. Таким чином, вона є фундаментальною частиною математичної освіти, що робить її вивчення вкрай важливим для майбутніх фахівців у наукових та інженерних дисциплінах.