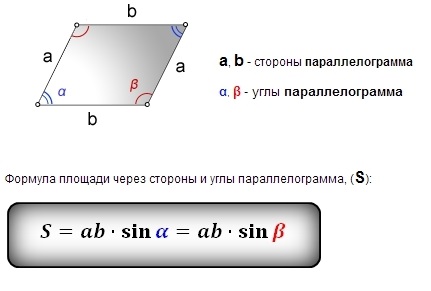
Формула площа паралелограма: детальний огляд
Формула площа паралелограма є фундаментальним поняттям в геометрії, яке дозволяє знаходити площу цього чотирикутника без особливих складнощів. Паралелограм є спеціальним типом чотирикутника, обидві пари протилежних сторін якого паралельні і рівні. Це означає, що даний полігон має певні властивості симетрії, які суттєво спрощують розрахунки, пов’язані з його площею.
Формула обчислення площі паралелограма
Основна формула для обчислення площі паралелограма виглядає наступним чином:
S = a ⋅ h
де:
- S – площа паралелограма,
- a – довжина основи паралелограма,
- h – висота, проведена до цієї основи.
Ця формула площа паралелограма є простою, але відзначається високим рівнем універсальності, оскільки вона застосовна до будь-якого паралелограма, незалежно від його форми та розмірів.
Доведення формули площі паралелограма
Розглянемо алгоритм виведення цієї формули:
- Зобразимо паралелограм ABCD з основою AB та висотою h, проведеною з вершини D на основу AB.
- Площа паралелограма ABCD дорівнює площі прямокутника, утвореного, якщо перетворити одну пару паралельних сторін у прямокутні.
- Таким чином, площа дорівнює добутку основи a на висоту h, що підтверджує основну формулу.
Цей процес демонструє, як паралельні сторони та висота формують прямолінійні межі фігури, полегшуючи обчислення.
Приклади розрахунків площі паралелограма
Давайте розглянемо кілька прикладів, аби закріпити розуміння використання формули:
| Приклад | Дані | Розрахунок | Результат |
|---|---|---|---|
| 1 | Основа a = 5 см, Висота h = 4 см | S = 5 см ⋅ 4 см | 20 см² |
| 2 | Основа a = 10 см, Висота h = 6 см | S = 10 см ⋅ 6 см | 60 см² |
Ці приклади ілюструють простоту обчислення з використанням формули для різних параметрів основи та висоти.
Застосування формули площі паралелограма в різних задачах
Формула площа паралелограма широко використовується у різних галузях, таких як архітектура, дизайн, фізика та навіть економіка. Незалежно від того, чи потрібно визначити площу поверхні будівлі чи витрати на матеріали, ця формула є незамінним інструментом.
Беручи до уваги надійність та універсальність основної формули, можна з упевненістю стверджувати, що площа паралелограма завжди буде ключовою частиною успішного вирішення різнопланових задач.