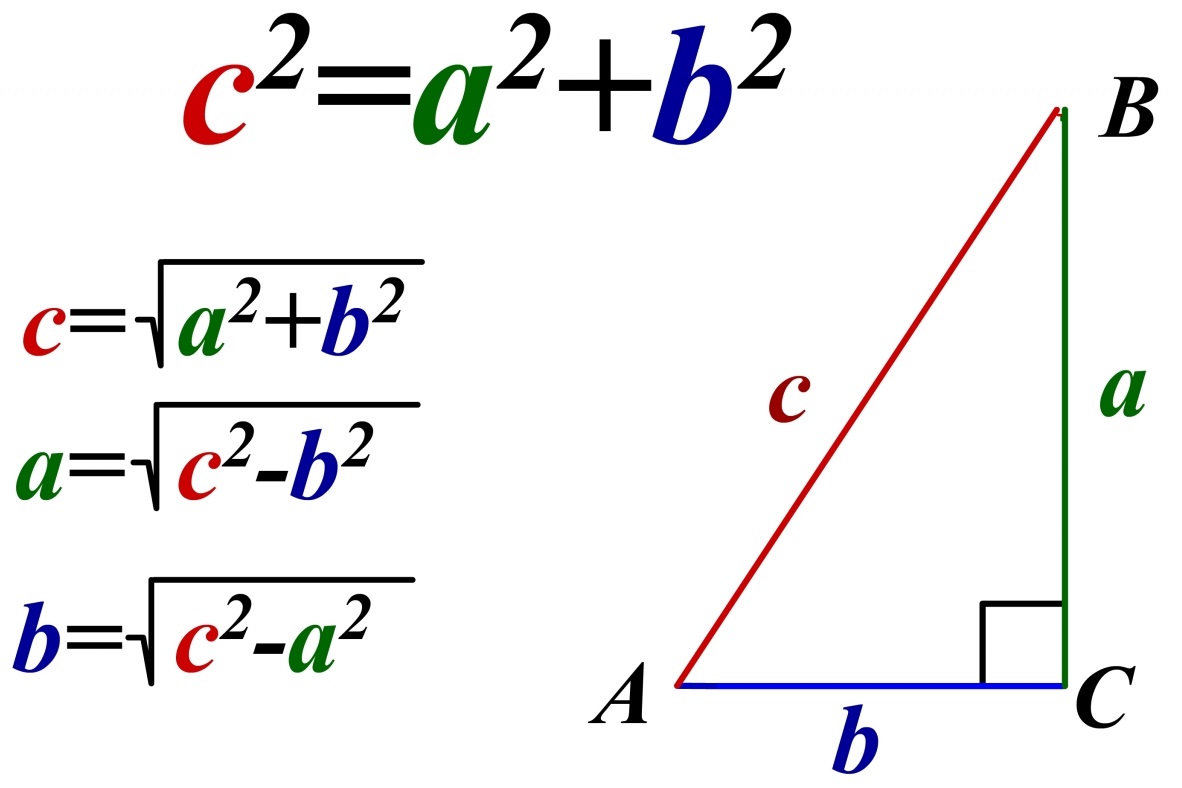Формула Піфагора: Основа Евклідової Геометрії
Формула Піфагора, або теорема Піфагора, є фундаментальним принципом у математиці, що відображає зв’язок між сторонами прямокутного трикутника. Ця теорема не лише допомагає у розв’язанні математичних задач, але й має безліч застосувань у фізиці, інженерії та навіть мистецтві. У цій статті ми розглянемо історію, застосування та докази одного з найвідоміших математичних принципів.
Історичний Контекст
Формула Піфагора датується VI століттям до нашої ери і приписується давньогрецькому ученому Піфагору Самоському. Це була унікальна епоха математичного розвитку, коли основи геометрії знаходили своє оформлення в абстрактних термінах. Проте, слід зауважити, що ця теорема була відома й іншим древнім цивілізаціям, таким як індійці та вавилоняни, задовго до Піфагора.
Формула і її основи
Формула Піфагора стверджує, що у прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів:
c2 = a2 + b2
- c – гіпотенуза, найдовша сторона трикутника.
- a і b – катети, які утворюють прямий кут.
Застосування формули
- Будівництво: Формула Піфагора використовується для визначення правильності кута в архітектурі.
- Астрономія: Обчислення відстаней між небесними об’єктами в тривимірному просторі.
- Комп’ютерна графіка: Використовується для обчислення реалістичної відстані між пікселями.
Докази Теореми
Існує безліч доказів цієї теореми як в геометричному, так і в алгебраїчному вимірах. Ось один з наочних геометричних доказів:
| Спосіб | Опис |
|---|---|
| Побудова на площині | Розбивається квадрат на ділянки, щоб візуально підтвердити рівність квадратів катетів і гіпотенузи. |
| Інтеграція | Використання аналітичної геометрії для підтвердження формули через інтеграцію функцій. |
Заключення
Формула Піфагора, незважаючи на свою простоту, є основою багатьох складних математичних концепцій. Її універсальність дозволяє використовувати в найрізноманітніших галузях науки і життя. Це підтверджує, що класична геометрія залишається актуальною навіть у наш час, формуючи наші уявлення про простір та форму. Теорема Піфагора є беззаперечним прикладом того, як давні знання можуть продовжувати впливати на сучасну науку і технологію.