Формула Комбинаторики: Вступ до Основ Теорії
Формула комбинаторики є ключовим інструментом у сфері математики, що дозволяє вирішувати завдання, пов’язані з обчисленням кількості можливих результатів. Розвиток комбинаторики надає змогу зрозуміти, як обчислювати кількість способів упорядкування, відбору та розміщення об’єктів.
Основи Комбинаторики
Комбинаторика як наука займається вивченням і визначенням кількості різних способів комбінацій елементів. Розглянемо ключові концепції, які становлять основу комбинаторики.
Перестановки
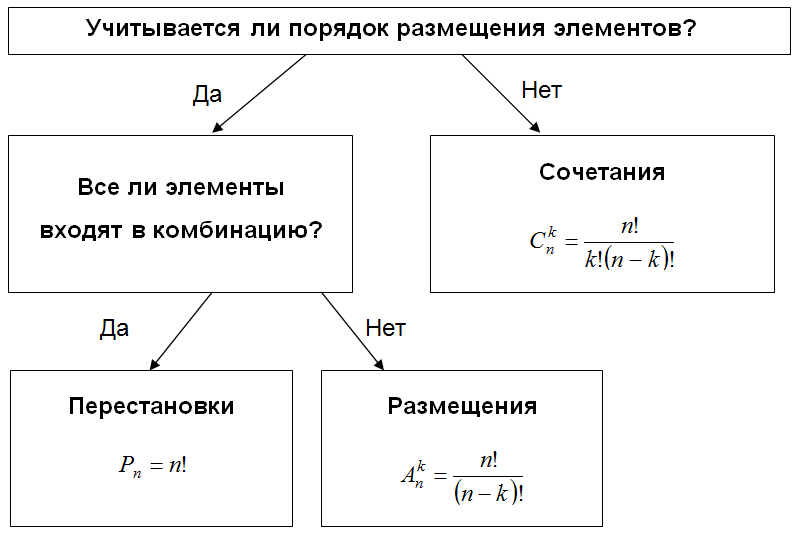
Перестановки стосуються порядкування всіх елементів набору. Формула для підрахунку кількості перестановок n елементів має вигляд n! (n факторіал), де:
- n! = 1 × 2 × 3 × … × n
Ця формула комбинаторики використовується, коли всі елементи набору мають бути використані.
Сполучення
Сполучення стосуються відбору k елементів з n без урахування порядку. Формула комбинаторики для визначення кількості сполучень виглядає так:
| Формула | Опис |
|---|---|
| C(n, k) = n! / (k! × (n-k)!) | Кількість способів вибору k елементів з n |
Розміщення
Розміщення використовуються, коли важливий порядок розташування k елементів з n. Формула для розміщення має вигляд:
A(n, k) = n! / (n-k)!
Цей підхід актуальний, коли позиції елементів у вибірці мають значення.
Основні Формули Комбинаторики в Застосуванні
Для багатьох математичних застосувань ключову роль відіграють класичні формули комбинаторики:
- Факторіал (n!): необхідний для базових розрахунків перестановок.
- Число сполучень (C): використовується, коли порядок не має значення.
- Число розміщень (A): підходить для задач, де порядок є критичним.
Ці формули активно використовуються в різних галузях, від комп’ютерних наук до теорії ймовірностей.
Практичне Застосування Формул Комбинаторики
Формула комбинаторики знаходить застосування у численних реальних сценаріях. Наведемо кілька прикладів:
- Криптографія: Визначення кількості можливих ключів в криптосистемах.
- Турнірне планування: Обчислення можливих матчів у спортивних заходах.
- Аналіз даних: Вибір підмножин даних для глибокого аналізу.
Знання та розуміння цих концепцій дозволяє з ефективністю вирішувати складні математичні проблеми в реальних умовах.
У висновку, формула комбинаторики є потужним інструментом для обчислень у багатьох сферах, допомагаючи швидко знаходити кількість можливих комбінацій, перестановок та розміщень. Це дозволяє вирішувати різноманітні завдання, які виникають у науці, техніці та повсякденному житті.