Теорема косинусів справджується: принципи та застосування
Теорема косинусів справджується в будь-якому трикутнику, що робить її універсальним інструментом для вирішення широкого спектра задач у планіметрії та аналітичній геометрії. Це одна з ключових теорем, яка дозволяє визначити довжини сторін чи величини кутів трикутника, якщо відомі деякі інші елементи.
Основи теореми косинусів
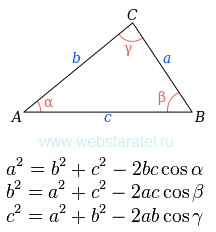
Теорема косинусів є узагальненням теореми Піфагора для будь-якого трикутника, не лише прямокутного. Вона стверджує, що для будь-якого трикутника з сторонами a, b і c, та відповідними протилежними кутами α, β і γ, виконується наступне рівняння:
| Формула |
|---|
| c² = a² + b² – 2ab*cos(γ) |
Іншими словами, квадрат будь-якої сторони трикутника дорівнює сумі квадратів інших двох сторін за вирахуванням подвоєного добутку цих сторін на косинус кута між ними.
Аналогії з теоремою Піфагора
Коли кут γ дорівнює 90°, косинус цього кута дорівнює нулю, і теорема косинусів перетворюється у відому теорему Піфагора:
- c² = a² + b², де γ = 90°
Це демонструє, як теорема косинусів поєднує в собі сміливість та витончення геометричні принципи.
Застосування теореми косинусів
Теорема косинусів є потужним інструментом, який використовується в різних ситуаціях. Ось декілька прикладів її застосування:
- Обчислення сторін трикутника: Коли відомі дві сторони трикутника і кут між ними, ми можемо скористатися теоремою косинусів, щоб знайти третю сторону.
- Визначення величини кутів: Коли відомі всі три сторони трикутника, теорема косинусів дозволяє обчислити косинуси кутів, а відповідно і самі кути.
- Розв’язання задач на рельєфі: В геодезії та картографії теорема косинусів застосовується для вимірювання відстаней на поверхні Землі, використовуючи координати точок.
Практичне розв’язання задач
Практичне застосування теореми показує, наскільки вона може бути корисною для розв’язання повсякденних задач. Наприклад:
- Навігація: Морські та авіаційні системи використовують триангуляцію, де важлива роль відводиться теоремі косинусів для визначення маршрутів та напрямків.
- Астрономія: Обчислення відстаней між космічними об’єктами у сферичній тригонометрії також може базуватися на принципах цієї теореми.
Висновок
Отже, теорема косинусів справджується в широкому діапазоні застосувань і забезпечує точність у розв’язанні геометричних задач. Вона з’єднує класичні принципи евклідової геометрії з сучасними технологічними інструментами для створення цінності в багатьох наукових та прикладних сферах. Кожен раз, використовуючи теорему косинусів, ми маємо можливість переконатися в її універсальності та надійності.